The polar moment of inertia is a measure of an object’s capacity to oppose or resist torsion when some amount of torque is applied to it on a specified axis. Torsion, on the other hand, is the twisting of an object due to an applied torque. The polar moment of inertia basically describes the cylindrical object’s (including its segments) resistance to torsional deformation when torque is applied in a plane that is parallel to the cross-section area or in a plane that is perpendicular to the object’s central axis.
If we put it in simple terms, the polar moment of inertia is the resistance offered by a beam or shaft when it is being distorted by torsion. This opposition usually arises from the cross-sectional area, and it should be noted that it does not depend on the material composition. If the polar moment of inertia is of a higher magnitude, then the torsional resistance of the object will also be greater. More torque will be required to turn the shaft at an angle.
Nonetheless, it is one of the main aspects of the area moment of inertia, and we can use the perpendicular axis theorem to link the two quantities.
Polar Moment of Inertia Formula
The Polar Moment of Inertia is also called the second polar moment of area. It is usually denoted by IZ. However, sometimes J or JZ is also used. The polar moment of inertia can be represented mathematically with the following formula:
| I or J = r2 dA |
Here,
r = distance to the element dA.
Units
The dimension unit of the polar moment of inertia is length to the power of four (L4). The SI unit of this property is metres to the fourth power (m4). In the imperial unit system, it is inches to the fourth power (in4).
Types of Cross-section Polar Moment of Inertia
There are three main types of cross-section polar moment of inertia. They are as follows.
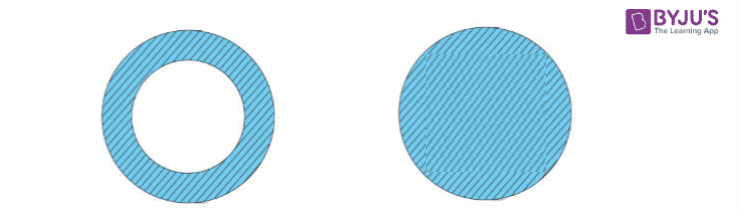
Hollow Cylinder Shaft and Solid Cylinder Shaft
1. Hollow Cylinder Shaft
To determine the polar moment of inertia, we use
Ro = inner radius of the hollow shaft
R1 = outer radius of the hollow shaft
3. Solid Cylinder Shaft
To determine the polar moment of inertia, we use the following formula:
R = radius of the circular shaft
2. Thin-Walled Shaft
To determine the polar moment of inertia, we use
t = thickness of the thin-walled shaft
Uses and Limitations
Generally, the second polar moment of area is used to determine the angular displacement of a body that is subjected to torque or to calculate the torsion force on a circular body. Because of the limitation, the polar moment of inertia is not suitable for analysing shafts and beams with non-circular cross-sections. This is mainly because objects with non-circular cross-sections tend to warp when torque is applied, and it further leads to out-of-plane deformations.
Difference between Moment of Inertia and Polar Moment of Inertia
While the moment of inertia and polar moment of inertia sound similar, they are two different quantities for measuring different properties of certain objects. We will look at a few differences below.
| Moment of Inertia | Polar Moment of Inertia |
| Moment of inertia is used to measure an object’s ability to oppose angular acceleration | It is a measurement of an object’s ability to oppose torsion |
| Its formula is given as I = r2 dm | It is defined as I or J = r2 dA |
| It is measured in kg m2 | Its SI unit is m4 |
| It depends on the mass of the body | It depends on the geometry of the body |
Frequently Asked Questions on Polar Moment of Inertia
How to find the polar moment of inertia?
The polar moment of inertia can be determined by taking the sum of the moments of inertia about two perpendicular axes lying in the plane of the cross-section that passes through this point.
What is the polar moment of inertia?
The polar moment of inertia is a measure of an object’s capacity to oppose or resist torsion when some amount of torque is applied to it on a specified axis.
What is the polar moment of inertia of a circle of diameter D?
πD4/32

Comments