Young's Double Slit Experiment

What Is Young’s Double Slit Experiment?

Young’s double slit experiment uses two coherent sources of light placed at a small distance apart. Usually, only a few orders of magnitude greater than the wavelength of light are used. Young’s double slit experiment helped in understanding the wave theory of light, which is explained with the help of a diagram. As shown, a screen or photodetector is placed at a large distance, ‘D’, away from the slits.

Download Complete Chapter Notes of Wave Optics
Download Now

JEE Main 2021 LIVE Physics Paper Solutions 24 Feb Shift-1 Memory-based

The original Young’s double slit experiment used diffracted light from a single source passed into two more slits to be used as coherent sources. Lasers are commonly used as coherent sources in modern-day experiments.

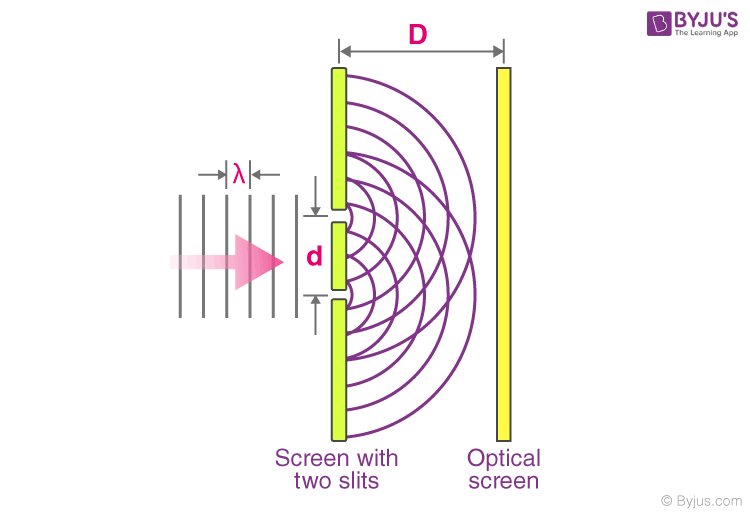
Youngs Double Slit Experiment image 1

Derivation
Position of Fringes
Shape of Fringes
Intensity of Fringes
Special Cases
Displacement of Fringes
Constructive and Destructive Interference

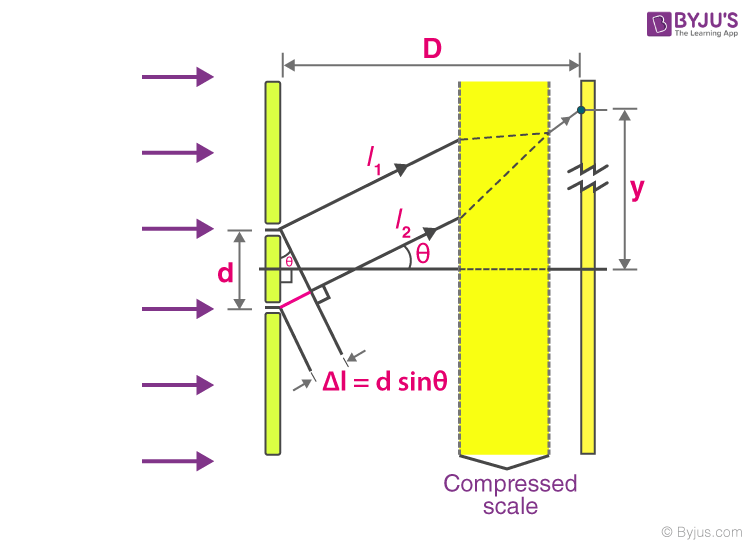
Each source can be considered a source of coherent light waves. At any point on the screen at a distance ‘y’ from the centre, the waves travel distances l₁ and l₂ to create a path difference of Δl at the point. The point approximately subtends an angle of θ at the sources (since the distance D is large, there is only a very small difference between the angles subtended at sources).

Derivation of Young’s Double Slit Experiment

Consider a monochromatic light source ‘S’ kept at a considerable distance from two slits: s₁ and s₂. S is equidistant from s₁ and s₂. s₁ and s₂ behave as two coherent sources as both are derived from S.

The light passes through these slits and falls on a screen which is at a distance ‘D’ from the position of slits s₁ and s₂. ‘d’ is the separation between two slits.

If s₁ is open and s₂ is closed, the screen opposite to s₁ is closed, and only the screen opposite to s₂ is illuminated. The interference patterns appear only when both slits s₁ and s₂ are open.

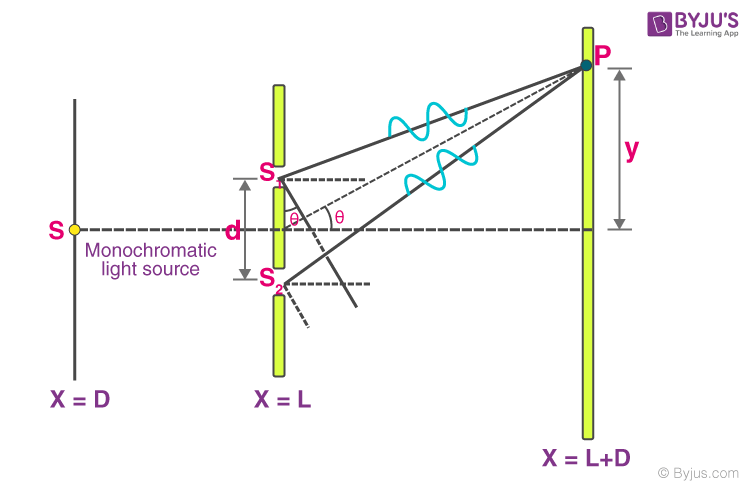
Youngs Double Slit Experiment image 3

When the slit separation (d) and the screen distance (D) are kept unchanged, to reach P, the light waves from s₁ and s₂ must travel different distances. It implies that there is a path difference in Young’s double slit experiment between the two light waves from s₁ and s₂.

Approximations in Young’s double slit experiment

Approximation 1:D > > d: Since D > > d, the two light rays are assumed to be parallel.
Approximation 2: d/λ >> 1: Often, d is a fraction of a millimetre, and λ is a fraction of a micrometre for visible light.

Under these conditions, θ is small. Thus, we can use the approximation sin θ = tan θ ≈ θ = λ/d.

∴ path difference, Δz = λ/d

This is the path difference between two waves meeting at a point on the screen. Due to this path difference in Young’s double slit experiment, some points on the screen are bright, and some points are dark.

Now, we will discuss the position of these light and dark fringes and fringe width.

Position of Fringes in Young’s Double Slit Experiment

Position of Bright Fringes

For maximum intensity or bright fringe to be formed at P,

Path difference, Δz = nλ (n = 0, ±1, ±2, . . . .)

i.e., xd/D = nλ

x = nλD/d

The distance of the n^thbright fringe from the centre is

x_n = nλD/d

Similarly, the distance of the (n-1)^th bright fringe from the centre is

x_(n-1)= (n -1)λD/d

Fringe width, β = x_n – x_(n-1)= nλD/d – (n -1)λD/d = λD/d

(n = 0, ±1, ±2, . . . .)

Position of Dark Fringes

For minimum intensity or dark fringe to be formed at P,

Path difference, Δz = (2n + 1) (λ/2) (n = 0, ±1, ±2, . . . .)

i.e., x = (2n +1)λD/2d

The distance of the n^thdark fringe from the centre is

x_n = (2n+1)λD/2d

Similarly, the distance of the (n-1)^th bright fringe from the centre is

x_(n-1)= (2(n-1) +1)λD/2d

Fringe width, β = x_n – x_(n-1)= (2n + 1) λD/2d – (2(n -1) + 1)λD/2d = λD/d

(n = 0, ±1, ±2, . . . .)

Fringe Width

The distance between two adjacent bright (or dark) fringes is called the fringe width.

β = λD/d

If the apparatus of Young’s double slit experiment is immersed in a liquid of refractive index (μ), then the wavelength of light and fringe width decreases ‘μ’ times.

\(\begin{array}{l}{{\beta }^{1}}=\frac{\beta }{\mu }\end{array} \)

If white light is used in place of monochromatic light, then coloured fringes are obtained on the screen, with red fringes larger in size than violet.

Angular Width of Fringes

Let the angular position of n^th bright fringe is θ_n,and because of its small value, tan θ_n ≈ θ_n

\(\begin{array}{l}\tan {{\theta }_{n}}=\frac{λn}{d}\end{array} \)

\(\begin{array}{l}\Rightarrow {{\theta }_{n}}= \frac{n\lambda }{d}\end{array} \)

Similarly, the angular position of (n+1)^th bright fringe is θ_n+1, then

\(\begin{array}{l}{{\theta }_{n+1}}=\frac{\left( n+1 \right)\lambda }{d}\end{array} \)

∴ The angular width of a fringe in Young’s double slit experiment is given by,

\(\begin{array}{l}\theta ={{\theta }_{n+1}}-{{\theta }_{n}}=\frac{\left( n+1 \right)\lambda }{d}-\frac{n\lambda }{d}=\frac{\lambda }{d}\end{array} \)

\(\begin{array}{l}\theta =\frac{\lambda }{d}\end{array} \)

We know that

\(\begin{array}{l}\beta =\frac{\lambda D}{d}\end{array} \)

\(\begin{array}{l}\Rightarrow \theta =\frac{\lambda }{d}=\frac{\beta }{D}\end{array} \)

Angular width is independent of ‘n’, i.e., the angular width of all fringes is the same.

Maximum Order of Interference Fringes

The position of n^th order maxima on the screen is

\(\begin{array}{l}\gamma =\frac{n\lambda D}{d};n=0,\pm 1,\pm 2, . . \end{array} \)

But ‘n’ values cannot take infinitely large values as it would violate the 2^nd approximation.

i.e., θ is small (or) y < < D

\(\begin{array}{l}\Rightarrow \frac{\gamma }{D}=\frac{n\lambda }{d}<<1\end{array} \)

Hence, the above formula for interference maxima is applicable when

\(\begin{array}{l}n<<\frac{d}{\lambda }\end{array} \)

When the ‘n’ value becomes comparable to d/λ, path difference can no longer be given by dγ/D.

Hence for maxima, path difference = nλ

\(\begin{array}{l}\Rightarrow d\sin \theta =n\lambda\end{array} \)

\(\begin{array}{l}\Rightarrow n=\frac{d\sin \theta }{\lambda }\end{array} \)

\(\begin{array}{l}{{n}_{\max }}=\left[ \frac{d}{\lambda } \right]\end{array} \)

The above represents the box function or greatest integer function.

Similarly, the highest order of interference minima

\(\begin{array}{l}{{n}_{\min }}=\left[ \frac{d}{\lambda }+\frac{1}{2} \right]\end{array} \)

The Shape of Interference Fringes in YDSE

From the given YDSE diagram, the path difference between the two slits is given by

\(\begin{array}{l}{{s}_{2}}p-{{s}_{1}}p\approx d\sin \theta\ (constant)\end{array} \)

The above equation represents a hyperbola with its two foci as, s₁ and s₂.

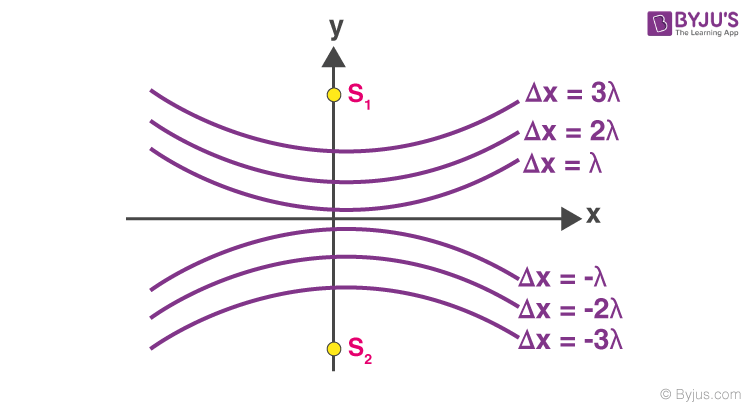
Youngs Double Slit Experiment image 4

The interference pattern we get on the screen is a section of a hyperbola when we revolve the hyperbola about the axis s₁s₂.

If the screen is a yz plane, fringes are hyperbolic with a straight central section.

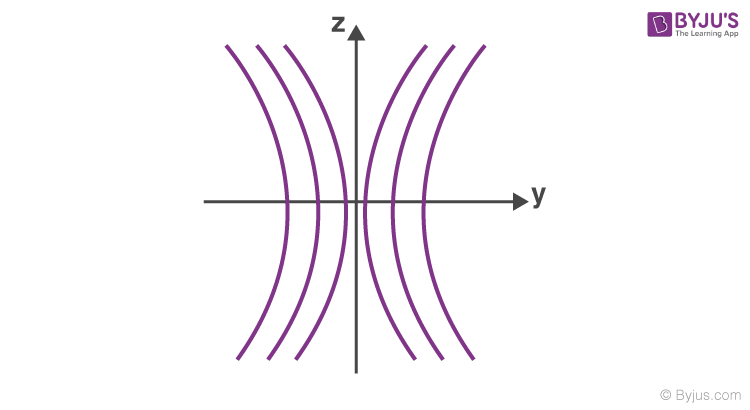
Youngs Double Slit Experiment image 5

If the screen is xy plane, the fringes are hyperbolic with a straight central section.

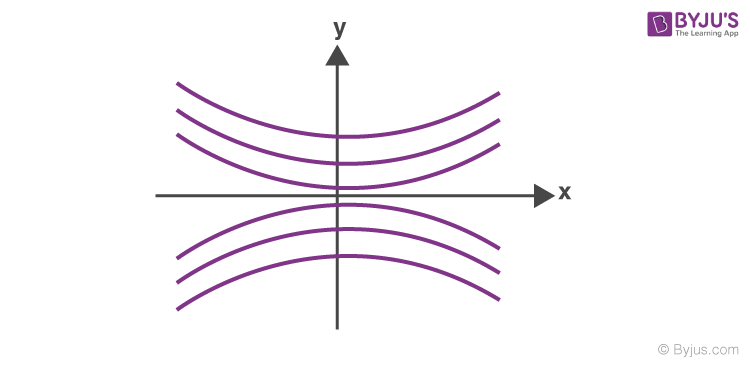
Youngs Double Slit Experiment image 6

The Intensity of Fringes in Young’s Double Slit Experiment

For two coherent sources, s₁ and s₂, the resultant intensity at point p is given by

I = I₁ + I₂ + 2 √(I₁ . I₂) cos φ

Putting I₁ = I₂ = I₀ (Since, d<<<D)

I = I₀ + I₀ + 2 √(I₀.I₀) cos φ

I = 2I₀ + 2 (I₀) cos φ

I = 2I₀ (1 + cos φ)

\(\begin{array}{l}I = 4{{I}_{0}}{{\cos }^{2}}\left( \frac{\phi }{2} \right)\end{array} \)

For maximum intensity

\(\begin{array}{l}\cos \frac{\phi }{2}=\pm 1\end{array} \)

\(\begin{array}{l}\frac{\phi }{2}=n\pi ,n=0,\pm 1,\pm 2,……\end{array} \)

or φ = 2nπ

phase difference φ = 2nπ

Then, path difference

\(\begin{array}{l}\Delta x=\frac{\lambda }{{2}{\pi }}\left( {2}n{\pi } \right)\end{array} \)

= nλ

The intensity of bright points is maximum and given by

I_max = 4I₀

For minimum intensity

\(\begin{array}{l}\cos \frac{\phi }{2}=0\end{array} \)

\(\begin{array}{l}\frac{\phi }{2}=\left( n-\frac{1}{2} \right)\pi \,\,\,\,\,where\,\left( n=\pm 1,\pm 2,\pm 3,….. \right)\end{array} \)

φ = (2n – 1) π

Phase difference φ = (2n – 1)π

\(\begin{array}{l}\frac{2\pi }{\lambda }\Delta x=\left( 2n-1 \right)\pi\end{array} \)

\(\begin{array}{l}\Delta x=\left( 2n-1 \right)\frac{\lambda }{2}\end{array} \)

Thus, the intensity of minima is given by

I_min = 0

If I₁ ≠ I₂, I_min ≠ 0.

Special Cases

Rays Not Parallel to Principal Axis:

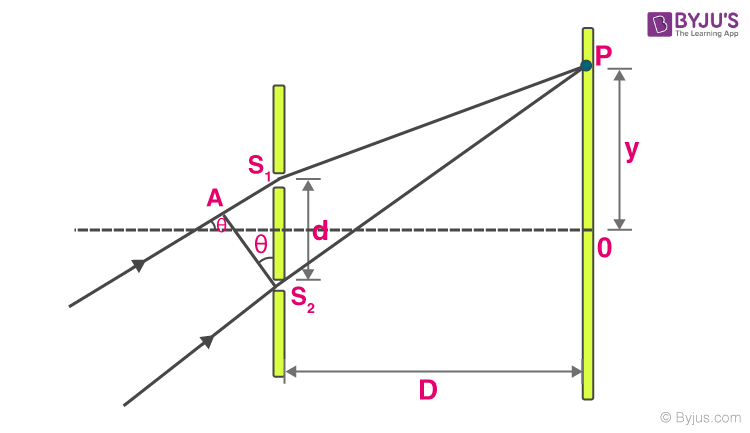
Youngs Double Slit Experiment image 7

From the above diagram,

Path difference

\(\begin{array}{l}\Delta x=\left( A{{S}_{1}}+{{S}_{1}}P \right)-{{S}_{2}}P\end{array} \)

\(\begin{array}{l}\Delta x=A{{S}_{1}}-\left( {{S}_{2}}P-{{S}_{1}}P \right)\end{array} \)

\(\begin{array}{l}\Delta x=d\sin \theta -\frac{4d}{D}\end{array} \)

For maxima

\(\begin{array}{l}\Delta x=n\lambda\end{array} \)

For minima

\(\begin{array}{l}\Delta x=\left( 2n-1 \right)\frac{\lambda }{2}\end{array} \)

Using this, we can calculate different positions of maxima and minima.

Source Placed beyond the Central Line:

If the source is placed a little above or below this centre line, the wave interaction with S₁ and S₂ has a path difference at point P on the screen.

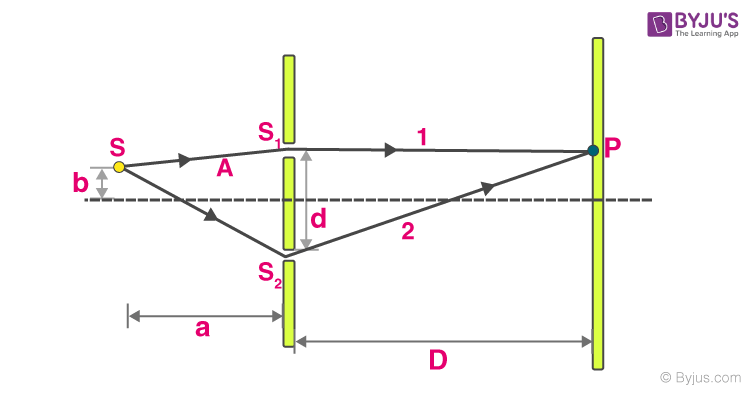
Youngs Double Slit Experiment image 8

Δ x= (distance of ray 2) – (distance of ray 1)

\(\begin{array}{l}=\left( S\,{{S}_{2}}+{{S}_{2}}P \right)-\left( S\,{{S}_{1}}+{{S}_{1}}P \right)\end{array} \)

\(\begin{array}{l}=\left( S\,{{S}_{2}}+S\,{{S}_{1}} \right)+\left( {{S}_{2}}P-{{S}_{1}}P \right)\end{array} \)

= bd/a + yd/D → (*)

We know Δx = nλ for maximum

Δx = (2n – 1) λ/2 for minimum

By knowing the value of Δx from (*), we can calculate different positions of maxima and minima.

Displacement of Fringes in YDSE

When a thin transparent plate of thickness ‘t’ is introduced in front of one of the slits in Young’s double slit experiment, the fringe pattern shifts toward the side where the plate is present.

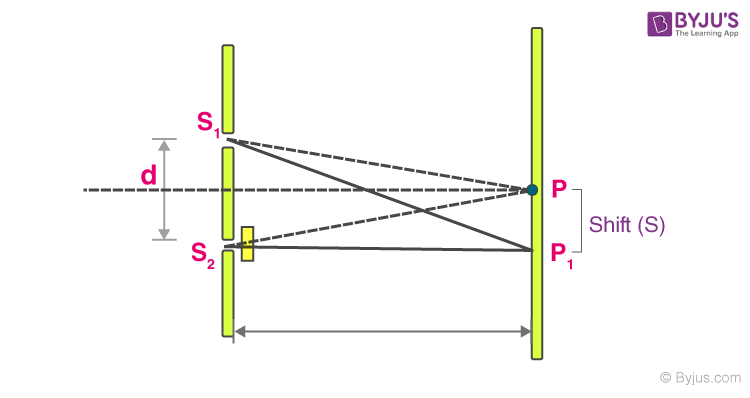
Youngs Double Slit Experiment image 9

The dotted lines denote the path of the light before introducing the transparent plate. The solid lines denote the path of the light after introducing a transparent plate.

Path difference before introducing the plate

\(\begin{array}{l}\Delta x={{S}_{1}}P-{{S}_{2}}P\end{array} \)

Path difference after introducing the plate

\(\begin{array}{l}\Delta {{x}_{new}}={{S}_{1}}{{P}^{1}}-{{S}_{2}}{{P}^{1}}\end{array} \)

The path length

\(\begin{array}{l}{{S}_{2}}{{P}^{1}}={{\left( {{S}_{2}}{{P}^{1}}-t \right)}_{air}}+{{t}_{plate}}\end{array} \)

\(\begin{array}{l}={{\left( {{S}_{2}}{{P}^{1}}-t \right)}_{air}}+{{\left( \mu t \right)}_{plate}}\end{array} \)

Where μt is the optical path.

\(\begin{array}{l}={{S}_{2}}{{P}^{1}}_{air}+\left( \mu -1 \right)t\end{array} \)

Then, we get,

\(\begin{array}{l}{{\left( \Delta x \right)}_{new}}={{S}_{1}}{{P}^{1}}_{air}-\left( {{S}_{2}}{{P}^{1}}_{air}+\left( \mu -1 \right)t \right)\end{array} \)

\(\begin{array}{l}={{\left( {{S}_{1}}{{P}^{1}}-{{S}_{2}}{{P}^{1}} \right)}_{air}}-\left( \mu -1 \right)t\end{array} \)

\(\begin{array}{l}{{\left( \Delta x \right)}_{new}}=d\sin \theta -\left( \mu -1 \right)t\end{array} \)

\(\begin{array}{l}{{\left( \Delta x \right)}_{new}}=\frac{\lambda d}{D}-\left( \mu -1 \right)t\end{array} \)

Then,

\(\begin{array}{l}\begin{matrix} y=\frac{\Delta xD}{d}+\frac{D}{d}\left[ \left( \mu -1 \right)t \right] \\ \downarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\downarrow \, \\ \left( 1 \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\,\,\,\, \\ \end{matrix}\end{array} \)

Term (1) defines the position of a bright or dark fringe; term (2) defines the shift that occurred in the particular fringe due to the introduction of a transparent plate.

Constructive and Destructive Interference

For constructive interference, the path difference must be an integral multiple of the wavelength.

Thus, for a bright fringe to be at ‘y’,

nλ = y d/D

Or, y = nλD/d

Where n = ±0,1,2,3…..

The 0th fringe represents the central bright fringe.

Similarly, the expression for a dark fringe in Young’s double slit experiment can be found by setting the path difference as

Δl = (2n+1)λ/2

This simplifies to

(2n+1)λ/2 = y d/D

y = (2n+1)λD/2d

Young’s double slit experiment was a watershed moment in scientific history because it firmly established that light behaved like a wave.

The double slit experiment was later conducted using electrons, and to everyone’s surprise, the pattern generated was similar as expected with light. This would forever change our understanding of matter and particles, forcing us to accept that matter, like light, also behaves like a wave.

Wave Optics