Wave undergoes phenomena like interference when it meets another wave. Interference definition states that it is a phenomenon in which two waves superpose with each other to form a resultant wave of lower, higher or of same amplitude.
There are two types of wave interference:
- Constructive interference
- Destructive interference
Constructive interference is a type of interference in which two interfering waves have a displacement in the same direction. In this article, let us understand the interference definition along with destructive interference in a detailed way.
| Table of Contents |
What is Destructive Interference?
Destructive interference occurs when waves come together so that they completely cancel each other out. When two waves destructively interfere, they must have the same amplitude in opposite directions.
There are many interesting wave phenomena in nature that cannot be defined by an individual wave. To comprehend the destructive interference phenomenon, we must examine based on the combination of waves. To examine these, we apply the principle of superposition which says:
“If two or more waves are traveling in a medium, the resulting wave function is the algebraic total of the individual waves function.”
When the waves of identical frequency and equivalent amplitude superimpose, the process of interference takes place. When two waves of a similar frequency move in a medium at the same time and in the same direction, because of their superposition, the resulting intensity of the medium at any point is dissimilar from the sum of their intensities. At some points, the strength of the resultant wave bears a larger value, while at certain points the value is very small.
Destructive Interference Representation
When two waves of similar frequencies travel in a medium, the resultant at different points is dissimilar from the sum of their intensities because of their superposition. At one point it is too less and negligible which we call Destructive Interference.
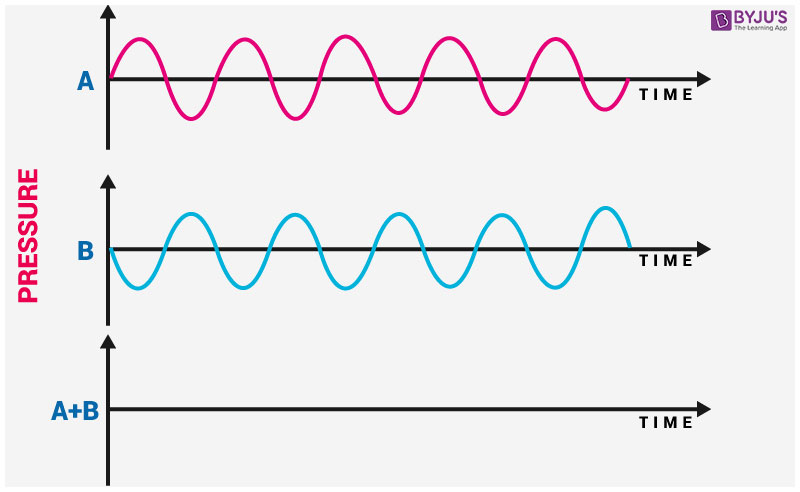
The crest of wave A overlaps with the trough of wave B and vice versa as a result of which they cancel each other out.
In the above figure, A and B are the two waves of similar frequencies travelling in a medium in a similar direction.
You may also want to check out these topics related to the concept of interference given below!
Destructive Interference Equation
The phase difference between two waves is an odd multiple of π that is:
The difference between the path of two waves is an odd multiple of λ/2,
The time interval among the two waves is an odd multiple of T/2,
The resultant amplitude is equivalent to the difference between the amplitudes of individual waves.
Examples of Destructive Interference
Some destructive interference examples are given below:
- Gravitational waves are a specimen of destructive interference.
- Light beams demonstrate destructive interference.
- Moving electrons and radio waves also perform destructive interference.
Read about: Coherent Sources and Sustained Interference
Frequently Asked Questions – FAQs
What is interference?
Interference is the phenomenon in which two waves superpose to form the resultant wave of the lower, higher or of the same amplitude.
What are the types of light interference?
The following are the types of light interference:
- Constructive interference
- Destructive interference
State the principle of superposition?
Can light waves undergo interference?
Can moving electrons and radio waves undergo destructive interference?
Hope you have understood about interference definition and destructive interference. Stay tuned to BYJU’S to learn more Physics concepts with the help of interactive video lessons.
Watch the video and understand the relationship between frequency and wavelength.


Comments