| Table of Contents |
Radiation Definition
Radiation is the transmission or emission of energy in the form of particles or waves through a material medium or space. The term radiation used here is another word for electromagnetic waves. These waves are formed due to the superposition of electric and magnetic fields perpendicular to each other, and carry energy.
In general, the word radiation has been adopted after the phenomenon of waves that usually tend to radiate from a source.
Important Types of Radiation
In Physics, we study different forms of radiation. The commons ones include
- Electromagnetic radiation: These include radiations such as microwaves, infrared, ultraviolet, radio waves, x-rays, gamma radiation (γ) and visible light.
- Particle radiation: These include alpha radiation (α), beta radiation (β) and neutron radiation.
- Acoustic radiation: Some of the popular ones are sound, ultrasound and seismic waves.
- Gravitational radiation: This is a type of radiation that often takes the form of gravitational waves or ripples in the curvature of spacetime.
Additionally, radiation is mainly described or divided into ionising or non-ionising radiation. This is done depending on the energy of the radiated particles.
Properties of Radiation
(a) All objects emit radiation simply because their temperature is above absolute zero, and all objects absorb some of the radiation that falls on them from other objects.
(b) Maxwell, on the basis of his electromagnetic theory, proved that all radiations are electromagnetic waves, and their sources are vibrations of charged particles in atoms and molecules.
(c) More radiations are emitted at a higher temperature of a body and lesser at a lower temperature.
(d) The wavelength corresponding to the maximum emission of radiation shifts from a longer wavelength to a shorter wavelength as the temperature increases. Due to this, the colour of a body appears to be changing. Radiations from a body at NTP have predominantly infrared waves.
(e) Thermal radiations travel with the speed of light and in a straight line.
(f) Radiations are electromagnetic waves and can also travel through a vacuum.
(g) Similar to light, thermal radiations can be reflected, refracted, diffracted and polarised.
(h) Radiation from a point source obeys inverse square law (intensity a 1/r2).
Also Read: Electromagnetic Spectrum and Electromagnetic Waves
Prevost Theory of Exchange
According to this theory, all bodies radiate thermal radiation at all temperatures. The amount of thermal radiation radiated per unit of time depends on the nature of the emitting surface, its area and its temperature. The rate is faster at higher temperatures. Besides, a body also absorbs part of the thermal radiation emitted by the surrounding bodies when this radiation falls on it.
If a body radiates more than what it absorbs, its temperature falls. If a body radiates less than what it absorbs, its temperature rises. And if the temperature of a body is equal to the temperature of its surroundings, it radiates at the same rate as it absorbs.
Black Body Radiation
(Fery’s black body)
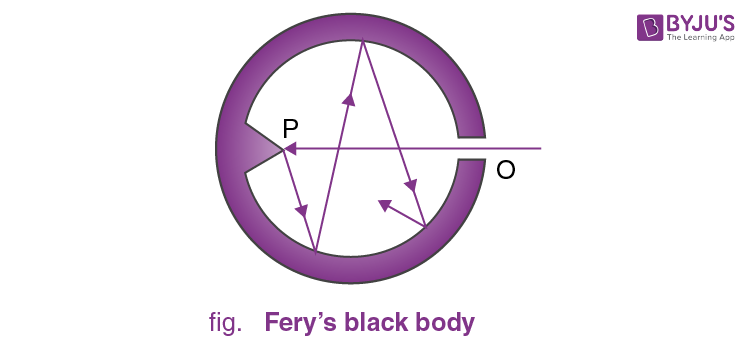
Perfectly Black Body
A perfectly black body is one which absorbs all the heat radiations of whatever wavelength incident on it. It neither reflects nor transmits any of the incident radiation, and therefore appears black, whatever the colour of the incident radiation.
In actual practice, no natural object possesses strictly the properties of a perfectly black body. But the lamp-black and platinum black are a good approximation of the black body. They absorb about 99 % of the incident radiation. The most simple and commonly used black body was designed by Fery. It consists of an enclosure with a small opening which is painted black from the inside. The opening acts as a perfect black body.
Any radiation that falls on the opening goes inside and has very little chance of escaping the enclosure before getting absorbed through multiple reflections. The cone opposite the opening ensures that no radiation is reflected back directly.
Black Body Radiation Video
Black Body Radiation

Absorption, Reflection and Emission of Radiations
Q = Qr + Qt + Qa
1 = r + t + a
Where r = Reflecting power , a = Absorptive power
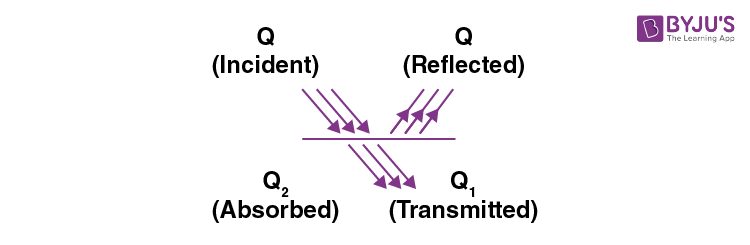
and t = Transmission power
(i) r = 0, t = 0, a = 1, perfect black body
(ii) r = 1, t = 0, a = 0, perfect reflector
(iii) r = 0, t = 1, a = 0, perfect transmitter
Absorptive Power
In particular, the absorptive power of a body can be defined as the fraction of incident radiation that is absorbed by the body.
As all the radiation incident on a black body is absorbed, a = 1 for a black body.
Emissive Power
Energy radiated per unit time per unit area, along the normal to the area, is known as emissive power.
(Notice that, unlike absorptive power, emissive power is not a dimensionless quantity).
Spectral Emissive Power (El)
Emissive power per unit wavelength range at wavelength l is known as spectral emissive power, El. If E is the total emissive power and El is the spectral emissive power, they are related as follows:
Emissivity
Kirchoff’s Law
The ratio of the emissive power to the absorptive power for the radiation of a given wavelength is the same for all substances at the same temperature, and is equal to the emissive power of a perfectly black body for the same wavelength and temperature.
Hence, we can conclude that good emitters are also good absorbers.
Read More: Kirchoff’s Law
Wien’s Displacement Law – Nature of Thermal Radiations
From the energy distribution curve of black body radiation, the following conclusions can be drawn:
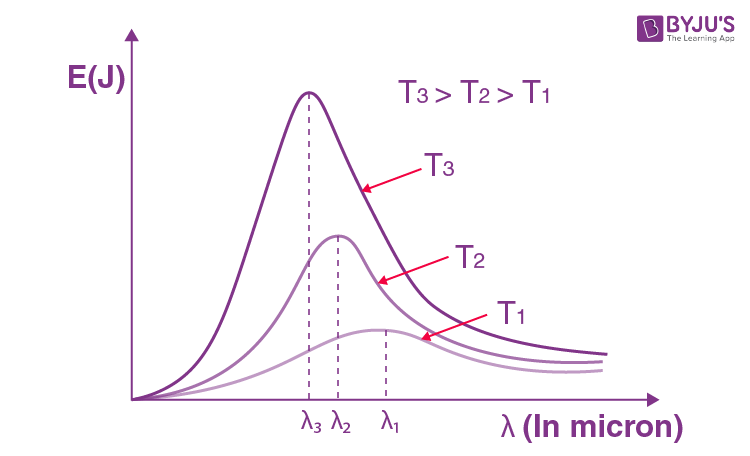
(a) The higher the temperature of a body, the higher the area under the curve, i.e., more amount of energy is emitted by the body at a higher temperature.
(b) The energy emitted by the body at different temperatures is not uniform. For both long and short wavelengths, the energy emitted is very small.
(c) For a given temperature, there is a particular wavelength (lm) for which the energy emitted (El) is maximum.
(d) With an increase in the temperature of the black body, the maxima of the curves shift towards shorter wavelengths.
From the study of the energy distribution of black body radiation, as discussed above, it was established experimentally that the wavelength (λm) corresponding to the maximum intensity of emission decreases inversely with the increase in the temperature of the black body, i.e.,
λm ∝ 1/T
λm = b/T
This is called Wien’s displacement law.
Here, b = 0.282 cm-K is Wien’s constant.
Ex: Solar radiation is found to have an intensity maximum near the wavelength range of 470 nm. Assuming the surface of the Sun to be perfectly absorbing (a = 1), calculate the temperature of the solar surface.
Sol. Since a =1, the Sun can be assumed to be emitting a black body.
From Wien’s law for a black body,
λmT = b
≃ 6125 K. Ans.
Applications of Radiation
- Radiation and radioactive substances are often used in the medical field for diagnosis, treatment and research. For example, X-rays and radiation therapy is used for cancer treatment.
- Electromagnetic radiation is used in almost all modern forms of communication systems.
- Radioactive atoms are used to determine the age of materials, such as in the process of carbon dating.
- Radiation is also used in determining the composition of materials. This process is termed neutron activation analysis.
On the other hand, radiation also has some harmful effects on living beings. They can cause burns or, in more serious cases, cancer or genetic damage. Radioactive waves are carcinogenic to humans.
Dual Nature of Radiation and Matter – Important Topics

Dual Nature of Radiation and Matter – Important Questions


Comments