JEE Main 2024 Question Paper Solution Discussion Live JEE Main 2024 Question Paper Solution Discussion Live
× Watch Now

Spring Mass System

Table of Contents

What Is Spring Mass System?

A spring-mass system, in simple terms, can be described as a spring system where a block is hung or attached at the free end of the spring. Usually, the spring-mass system is used to find the period of any object performing the simple harmonic motion. The spring-mass system can also be used in a wide variety of applications. For instance, a spring-mass system can be used to simulate the motion of human tendons using computer graphics as well as foot skin deformation.

Vertical spring-mass system

How Does Mass Affect the Period of a Spring?

Consider a spring with mass m with spring constant k; in a closed environment, the spring demonstrates a simple harmonic motion.

T = 2π √m/k

From the above equation, it is clear that the period of oscillation is free from both gravitational acceleration and amplitude. Also, a constant force cannot alter the period of oscillation. Meanwhile, the time period is directly proportional to the mass of the body that is fixed to the spring. When a heavy object is attached to it, it will oscillate more slowly.

Spring Mass System Arrangements

Spring mass systems can be arranged in two ways, and they are as follows:

  • The parallel combination of springs

  • The series combination of springs

We will discuss them below.

Parallel Combination of Springs

Parallel Combination of Springs

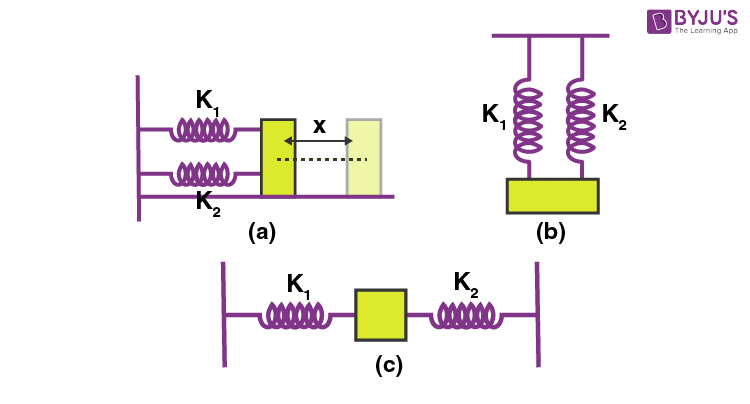
Fig (a), (b) and (c) are the parallel combination of springs.

Displacement on each spring is the same.

But restoring force is different.

\(\begin{array}{l}F={{F}_{1}}+{{F}_{2}}\end{array} \)

Since F = -kx, the above equation can be written as

\(\begin{array}{l}\Rightarrow -{{k}_{p}}x=-{{k}_{1}}x-{{k}_{2}}x\end{array} \)
\(\begin{array}{l}\Rightarrow -x{{k}_{p}}=-x\left( {{k}_{1}}+{{k}_{2}} \right)\end{array} \)
\(\begin{array}{l}\Rightarrow {{k}_{p}}={{k}_{1}}+{{k}_{2}}\end{array} \)

Also Read:

Time Period in Parallel Combination

\(\begin{array}{l}T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{m}{{{k}_{p}}}}=2\pi \sqrt{\frac{m}{{{k}_{1}}+{{k}_{2}}}}\end{array} \)

Springs in Series Combination

Springs in Series Combination

The force on each string is the same, but the displacement on each string is different.

\(\begin{array}{l}x={{x}_{1}}+{{x}_{2}}\end{array} \)

Since F = -kx, the above equation can be written as

\(\begin{array}{l}\frac{F}{-k_{s}}= \frac{F}{-k_{1}}+\frac{F}{-k_{2}}\end{array} \)

 

\(\begin{array}{l}\frac{1}{k_{s}}= \frac{1}{k_{1}}+\frac{1}{k_{2}}\end{array} \)
\(\begin{array}{l}\Rightarrow {{k}_{s}}=\frac{{{k}_{1}}{{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}\end{array} \)

Time Period in Series Combination

\(\begin{array}{l}T=2\pi \sqrt{\frac{m}{{{k}_{s}}}}=2\pi \sqrt{\frac{m\left( {{k}_{1}}+{{k}_{2}} \right)}{{{k}_{1}}{{k}_{2}}}}\end{array} \)

Spring Constant

From Hooke’s law,

Youngs modulus of elasticity,

\(\begin{array}{l}Y=\frac{Stress}{Strain}=\frac{\frac{F}{A}}{\frac{\Delta L}{L}}\end{array} \)

Here,

F = Force needed to extend or compress the spring

A = area over which the force is applied

L = nominal length of the material

ΔL = change in the length

\(\begin{array}{l}\frac{Y\Delta L}{L}=\frac{F}{A}\end{array} \)
\(\begin{array}{l}F=\frac{YA}{L}\left( \Delta L \right)\end{array} \)

Here,

\(\begin{array}{l}K=\frac{YA}{L}\end{array} \)
\(\begin{array}{l}\Rightarrow K\propto \frac{1}{L}\end{array} \)

Therefore, the above equation can be written as

\(\begin{array}{l}\Rightarrow F=K\,x\end{array} \)

If a spring of spring constant (K) and length (L) is cut into L/2 size two pieces, then what will be the magnitude of the spring constant of the new pieces?

Springs constant k

\(\begin{array}{l}K\propto \frac{1}{L}\end{array} \)
then K becomes = 2K for the new pieces.

Spring Constant Video

Understanding Spring Constant

How to Find the Time Period of a Spring Mass System?

Spring Mass System

Steps:

1. Find the mean position of the SHM (the point at which Fnet = 0) in the horizontal spring-mass system.

The natural length of the spring = the position of the equilibrium point.

2. Displace the object by a small distance (x) from its equilibrium position (or) mean position. The restoring force for the displacement ‘x’ is given as,

F = -k{x}….(1)

The acceleration of the body is given as a = F/m

Substituting the value of F from equation (1), we get

\(\begin{array}{l}a=\frac{-kx}{m}\end{array} \)

The acceleration of the particle can be written as

\(\begin{array}{l}a=-{{\omega }^{2}}x….(2)\end{array} \)

Equating equations (1) and (2),

\(\begin{array}{l}\frac{-k}{m}x=-{{\omega }^{2}}x\end{array} \)
\(\begin{array}{l}\Rightarrow \omega =\sqrt{\frac{k}{m}}\end{array} \)

Substitute ω value in standard time period expression of SHM

\(\begin{array}{l}T=\frac{2\pi }{\omega }=\frac{2\pi }{\sqrt{\frac{k}{m}}}=2\pi \sqrt{\frac{m}{k}}\end{array} \)
\(\begin{array}{l}T=2\sqrt{\frac{Mass}{Force\,constant}}\end{array} \)

Problems on Spring Mass System

Q.1: A particle is executing linear SHM. What are its velocity and displacement when its acceleration is half the maximum possible?

Solution:

\(\begin{array}{l}\overrightarrow{a}=-A{{\omega }^{2}}\sin \left( \omega t+\phi \right)\end{array} \)
\(\begin{array}{l}\Rightarrow \overrightarrow{{{a}_{\max }}}=-A{{\omega }^{2}}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{{{a}_{\max }}}{2}=-\frac{A{{\omega }^{2}}}{2}=-A{{\omega }^{2}}\sin \left( \frac{\pi }{6} \right)\end{array} \)

Phase

\(\begin{array}{l}\left( \omega t+\phi \right)=\frac{\pi }{6}\end{array} \)
\(\begin{array}{l}\Rightarrow v=A\omega \cos \left( \frac{\pi }{6} \right)=A\omega \frac{\sqrt{3}}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow x=A\sin \left( \frac{\pi }{6} \right)=\frac{A}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow \left( v=A\omega \frac{\sqrt{3}}{2},\,and\,\,x=\frac{A}{2} \right)\end{array} \)

Q.2: A particle executing linear SHM has speeds v1 and v2 at distances y1 and y2 from the equilibrium position. What is the frequency of the oscillation of the particle?

Solution:

\(\begin{array}{l}v=\omega \sqrt{{{A}^{2}}-{{y}^{2}}}\end{array} \)
\(\begin{array}{l}\Rightarrow {{v}^{2}}={{\omega }^{2}}\left( {{A}^{2}}-{{y}^{2}} \right)\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{{{v}^{2}}}{{{\omega }^{2}}}=\left( {{A}^{2}}-{{y}^{2}} \right)\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{{{v}^{2}}}{{{\omega }^{2}}}+{{y}^{2}}={{A}^{2}}….(1)\end{array} \)
\(\begin{array}{l}\Rightarrow {{A}^{2}}=\frac{v_{1}^{2}}{{{\omega }^{2}}}+y_{1}^{2}=\frac{v_{2}^{2}}{{{\omega }^{2}}}+y_{2}^{2}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{v_{1}^{2}-v_{2}^{2}}{{{\omega }^{2}}}=y_{2}^{2}-y_{1}^{2}\end{array} \)
\(\begin{array}{l}\Rightarrow {{\omega }^{2}}=\frac{v_{1}^{2}-v_{2}^{2}}{y_{2}^{2}-y_{1}^{2}}\end{array} \)
\(\begin{array}{l}\Rightarrow \omega =2\pi f\end{array} \)
\(\begin{array}{l}\Rightarrow f=\frac{\omega }{2\pi }=\frac{1}{2\pi }{{\left[ \frac{v_{1}^{2}-v_{2}^{2}}{y_{2}^{2}-y_{1}^{2}} \right]}^{\frac{1}{2}}}\end{array} \)

Q.3: A particle is executing SHM of amplitude A.

(a) What fraction of the total energy is kinetic when displacement is a quarter of the amplitude?

(b) At what displacement is the energy half kinetic and half potential?

Solution:

\(\begin{array}{l}KE=\frac{1}{2}m{{\omega }^{2}}\left( {{A}^{2}}-{{y}^{2}} \right)\end{array} \)
\(\begin{array}{l}\Rightarrow PE=\frac{1}{2}m{{\omega }^{2}}{{y}^{2}}\end{array} \)
\(\begin{array}{l}\Rightarrow E=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\end{array} \)

(a) at

\(\begin{array}{l}y=\frac{A}{4},\end{array} \)
KE becomes

\(\begin{array}{l}KE=\frac{1}{2}m{{\omega }^{2}}\left( {{A}^{2}}-{{\left( \frac{A}{4} \right)}^{2}} \right)\end{array} \)
\(\begin{array}{l}= \frac{15}{16}\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\end{array} \)

= [(15/16) x 100] % of  E

= 93% of total energy is KE

(b) KE = PE

\(\begin{array}{l}\frac{1}{2}m{{\omega }^{2}}\left( {{A}^{2}}-{{y}^{2}} \right)=\frac{1}{2}m{{\omega }^{2}}{{y}^{2}}\end{array} \)
\(\begin{array}{l}y=\frac{A}{\sqrt{2}}\end{array} \)

Q.4: Three springs, each of force constant k, are connected at equal angles with respect to each other to a common mass. If the mass is pulled by any one of the springs, then what is the time period of its oscillation?

\(\begin{array}{l}(a)\ 2\pi \sqrt{\frac{M}{K}}\end{array} \)
\(\begin{array}{l}(b)\ 2\pi \sqrt{\frac{M}{2K}}\end{array} \)
\(\begin{array}{l}(c)\ 2\pi \sqrt{\frac{2M}{3K}}\end{array} \)
\(\begin{array}{l}(d)\ 2\pi \sqrt{\frac{2M}{K}}\end{array} \)

 

Spring Mass System Solved Examples

Solution:

It is pulled by an upper spring, each making equal angles.

Spring Mass System Solved Examples

\(\begin{array}{l}\cos 60{}^\circ =\frac{\Delta x}{x}\end{array} \)
\(\begin{array}{l}\Rightarrow x\cos 60{}^\circ =\Delta \,x\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{x}{2}=\Delta \,x\end{array} \)

Spring Mass System Solved Examples

\(\begin{array}{l}{{F}_{net}}=Kx+2\frac{Kx}{2}\cos 60{}^\circ\end{array} \)
\(\begin{array}{l}= Kx+\frac{Kx}{2}=\frac{3Kx}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow {{K}_{eqn}}x=\frac{3Kx}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow {{K}_{eqn}}=\frac{3K}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow T=2\pi \sqrt{\frac{M}{K}}=2\pi \sqrt{\frac{2M}{3K}}\end{array} \)

Q.5: A particle of mass 0.2 kg is executing SHM of amplitude 0.2 m. When the particle passes through the mean position, its mechanical energy is 4 × 10-3 J. Find the equation of motion of the particle if the initial phase of oscillation is 60°.

\(\begin{array}{l}(a)\ 0.1\sin \left( 2t+\frac{\pi }{4} \right)\end{array} \)
\(\begin{array}{l}(b)\ 0.2\sin \left( \frac{1}{2}t+\frac{\pi }{3} \right)\end{array} \)
\(\begin{array}{l}(c)\ 0.2\sin \left( t+\frac{\pi }{3} \right)\end{array} \)
\(\begin{array}{l}(d)\ 0.1\cos \left( 2t+\frac{\pi }{4} \right)\end{array} \)

Solution:

The equation of motion of the particle is

\(\begin{array}{l}y=A\sin \left( \omega t+\phi \right)\end{array} \)

A = 0.2 m,

\(\begin{array}{l}\omega =?,\,\,\phi =60{}^\circ ,\,\,ME=4\times {{10}^{-3}}J\end{array} \)

From energy

\(\begin{array}{l}E=\frac{1}{2}m{{\omega }^{2}}{{A}^{2}}\end{array} \)
,

\(\begin{array}{l}4\times {{10}^{-3}}=\frac{1}{2}\left( 0.2 \right){{\omega }^{2}}{{\left( 0.2 \right)}^{2}}\end{array} \)
,

\(\begin{array}{l}{{\omega }^{2}}=\frac{4\times {{10}^{-3}}\times 2}{\left( 0.2 \right){{\left( 0.2 \right)}^{2}}}=\frac{8\times {{10}^{-3}}}{0.008}=1\,rad\,{{s}^{-1}}\end{array} \)
,

\(\begin{array}{l}y=0.2\sin \left( t+\frac{\pi }{3} \right)\end{array} \)

Q.6: A block of mass 0.1 kg, which slides without friction on a 30° incline, is connected to the top of the incline by a massless spring of force constant 40 Nm-1. If the block is pulled slightly from its mean position, what is the period of oscillation?

Spring Mass System Solved Examples

(a) π s

(b) π/10 s

(c) 2π/5 s

(d) π/2 s

Solution:

\(\begin{array}{l}T=2\pi \sqrt{\frac{M}{K}}=2\pi \sqrt{\frac{0.1}{40}}\end{array} \)
\(\begin{array}{l}=\frac{\pi }{10}s\end{array} \)

Frequently Asked Questions on Spring Mass System

Q1

The mass of the bob has no effect on the duration of oscillation of a basic pendulum. The period of a mass-spring system, on the other hand, is determined by mass. Explain the apparent contradiction.

Because the mass has to “count” for two different things, the basic pendulum has no reliance on mass. Inertia, or the “m” in “F=ma,” is measured by mass. The same thing happens in freefall, where everything falls at the same rate regardless of weight. This means that the resistance to motion changes is proportional to the mass. However, an object’s weight (force) is proportional to its mass. Because mass influences both the cause and resistance to change in motion, it cancels out.

The mass of a mass-spring system influences the inertia, but it does not create the force. Force is entirely due to the spring (and its spring constant). So, mass solely affects resistance to accelerations, and the slower the object wiggles back and forth, the more massive it is.

Q2

Explain how, despite the fact that the distance travelled during each cycle is related to the amplitude, the period of a mass-spring system can be independent of it.

When the distance travelled by the mass is increased, more energy is put into the system. As a result, it moves more quickly on average. It turns out that the amount it moves faster is just right to compensate for the additional distance it must travel.

Q3

What are the factors that affect the period of a mass oscillating on a spring?

The period of a mass oscillating on a spring is given by
T = 2π√(m/k)
m is the mass
k is the spring constant
As can be seen, both the mass and the spring constant influence the period of mass oscillation on the spring.

Test your Knowledge on Spring mass system
Quiz Image

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz

Congrats!

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

0 out of 0 arewrong
0 out of 0 are correct
0 out of 0 are Unattempted

Comments

Leave a Comment

Your Mobile number and Email id will not be published.

*

*