Moment of inertia of a rectangle along with its formulas with respect to different situations is discussed here. There are generally three situations that we will discuss in this lesson.
1. An Axis Passing Through Its Centroid
When we take a situation when the axis passes through the centroid, the moment of inertia of a rectangle is given as:
| I = bh3 / 12 |
Here, b is used to denote the rectangle width (the dimension parallel to the axis) and h is said to be the height (dimension perpendicular to the axis).
2. An Axis Passing Through Its Base
If we talk about an axis passing through the base, the moment of inertia of a rectangle is expressed as:
| I = bh3 / 3 |
This can be easily determined by the application of the Parallel Axis Theorem since we can consider that the rectangle centroid is located at a distance equal to h/2 from the base.
Parallel Axis Theorem
If we take the parallel axis theorem it can be used in determining the area moment of inertia of any shape that is present in any parallel axis. Here, we can find the non-centroidal axis if we know its moment of inertia with respect to a centroidal axis that is parallel to the first one. Usually, the equation is given as;
| I = Ix + Ad2 |
Ix = moment of inertia in arbitrary axis
A = area of the shape
D = the perpendicular distance between the x and x’ axes.
3. A Centroidal Axis Perpendicular To Its Base
When we take the centroidal axis perpendicular to its base, the moment of inertia of a rectangle can be determined by alternating the dimensions b and h, from the first equation that is given above. We will get the following equation;
| Iy = hb3/ 12 |
Calculating Moment Of Inertia Of Rectangle Section
We will learn how to calculate the moment of inertia of a rectangle section below.
We will take one rectangular section ABCD as depicted in the figure given below. Now we will assume that one of the lines will pass through the base of the rectangular section. We will take this line to be the line CD. Now, we will determine the area moment of inertia for the rectangular section about this line CD.
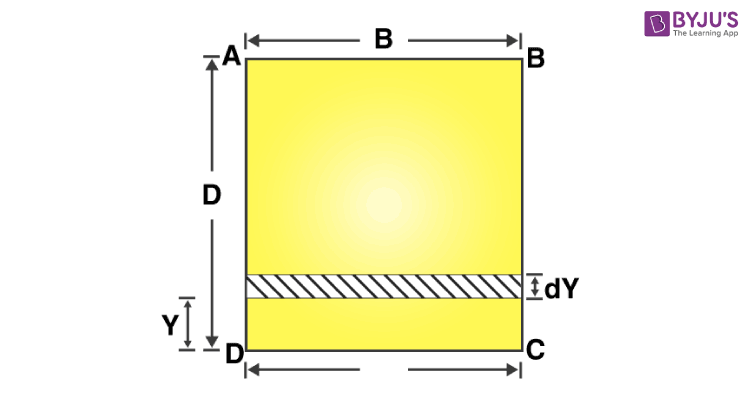
B = Width of the ABCD rectangular section
D = Depth of the ABCD rectangular section
ICD = Moment of inertia of the rectangular section about the CD line
The next step involves determining the value or expression for the moment of inertia of the rectangular plate about the line CD. Here we will take one rectangular elementary strip with a thickness dY that will be at a distance Y from the line CD. This can be seen in the above figure.
Area of the rectangular elementary strip is given as dA = dY.B
Moment of inertia about the line CD = dA.Y2 = B Y2 dY
After finding the moment of inertia of the rectangular section about the line CD we will move on to finding the moment of inertia of the entire area of the rectangular section about the line CD. We will integrate the above equation between limit 0 to D.
The moment of inertia of the entire area of the rectangular section about the line CD is usually given as;
ICD = O ∫D B Y2 dY
ICD = B O ∫D Y2 dY
ICD = B [y3 / 3]OD
ICD = BD3 / 3
The moment of inertia of the rectangular section about the line CD
ICD = BD3 / 3
⇒ Check Other Object’s Moment of Inertia:
- Moment Of Inertia Of A Cylinder
- Moment Of Inertia Of A Solid Cylinder
- Moment Of Inertia Of A Rectangular Plate
- Moment Of Inertia Of Triangle
- Moment Of Inertia Of Rod
Parallel Axis theorem

Comments