Moment Of Inertia Of Solid Cone

Moment of inertia of solid cone can be expressed using the given formula;

However, in this lesson, we will understand how the formula is derived and used in solving the problems. Let us first go through the derivation of the moment of inertia formula for a solid cone.

Solid Cone Moment Of Inertia Formula Derivation

We will take a solid cone where its axis will pass through the centre with radius = r, height = h. We will divide the cone into a small elemental disc where we consider the cone’s radius to be r and of thickness dz. We will need to determine the mass though.

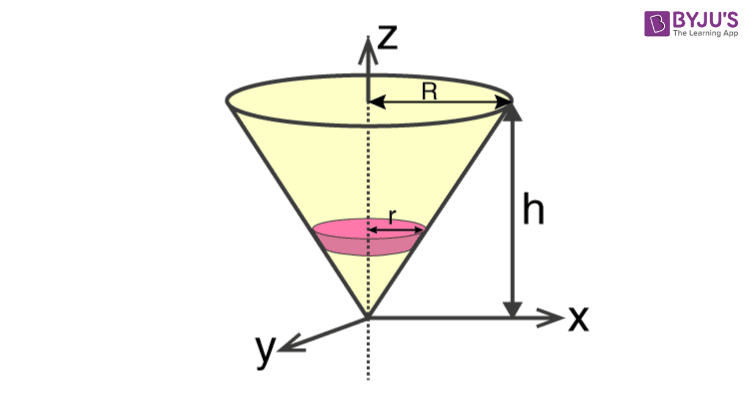
We take the elemental disc whose mass is given by;

dm = ρ ⋅ π r²dz

Density is given as;

ρ = M / V = M / (⅓ π R²h)

With this, we will calculate the dm.

dm = [M / (⅓ π R²h)] . ( π r²dz)

dm = (3M / R²h) . (r²dz)

If we consider the similarity of the triangle, then we have;

R / r = h / z

r = R X (z / h)

Now,

dm = (3M / R²h ) . (R² ⋅ z²/ h² )dz

dm = (3M z² / h³) dz

If we consider z-axis, the moment of inertia of the elemental disk will be;

dI = (½) dmr²

dI = (½ )⋅ (3M z²/ h³ ) ⋅ (z² R² / h² )dz

dI = (3 M R² /2 h⁵ ).  z⁴ dz

Now we will follow the integration process. Here;

I =(3 M R² /2 h⁵ )  _o∫^h z⁴dz

I = (3 M R² /2 h⁵ ). [z⁵ / 5 ]_o^h

I = (3 M R² /2 h⁵ )⋅ (h⁵ / 5)

Therefore, I = 3 MR²/10 

⇒ Check Other Object’s Moment of Inertia:

• Moment Of Inertia Of An Ellipse
• Moment Of Inertia Of A Cone
• Moment Of Inertia Of Hollow Cone
• Moment Of Inertia Of Circle
• Moment Of Inertia Of Ring