Moment Of Inertia Of A Cube

Moment of inertia of cube can be calculated using different equations depending on the location of the axis. Normally, there are two instances that we consider. They are;

• When the axis of rotation is at the centre. The formula is given as;

• When the axis passes through the edge. The moment of inertia is calculated using the following expression;

Moment Of Inertia Of Cube Derivation

1. To derive the moment of inertia of a cube when its axis is passing through the centre we have to consider a few things. We will assume the solid cube having mass m, height h, width w, and depth d. Interestingly, the cube’s moment of inertia will be similar to that of a square lamina with side about an axis through the centre.

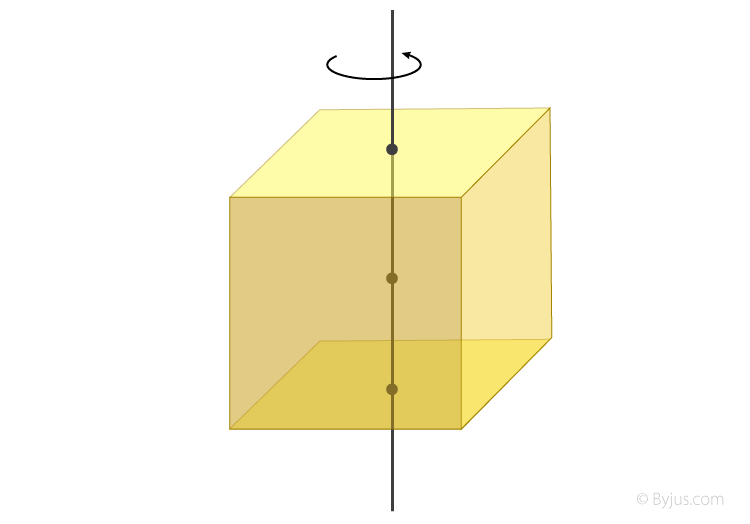
Now we will assume the area density of the lamina to be ρ. We will then take the element of the lamina with cartesian coordinates x, y in the plane to be dx dy. Now we can assume its mass to be = ρdxdy.

When we are finding the MOI we will use ρ(x²+y²) dx dy.

Next step involves integration where we integrate over the entire lamina. We obtain;

_–-a/2∫^a/2 ρ (x²+y²) dx dy = ρa⁴ / 6.

We will then substitute the values for the mass of the lamina which is ρ =ma².

And we obtain, I = ma² / 6

2. For the second instance when the axis is passing through the edge we will understand how the derivation is carried out below.

First, we recall the equation for moment of inertia. It is written as;

I = ∫ r²dm

Now since we need to find the MOI about an axis through the edge, we will take the z-axis.

Moving forward, we have to consider the cube to be broken down into infinitesimally small masses. We can then assume their sizes to be dy, dx, and dz. With this we get;

dm = ρ dxdydz

Here, ρ = density.

If we look at the moment of inertia formula given above we have r as well. It is nothing but the distance from the z-axis to mass dm. Consider the coordinates of the mass ‘dm’ to be x,y, and z). Now the distance ‘r’ will be;

r= √ x² + y²

r² = x² + y²

Meanwhile, the value of x,y, and z will range from O to b according to the length of the edges.

We will now substitute the values that we have got so far in the moment of inertia equation and also carry out the integration.

I = ∫ r²dm

I = _o∫^b _o∫^b _o∫^b (x² + y²) ρdxdydz

I = ρ 2b⁵ / 3

Mass of cube, m = ρb³.

If we substitute it in the equation, we obtain;

I = 2mb² / 3

⇒ Check Other Object’s Moment of Inertia:

• Moment Of Inertia Of An Ellipse
• Moment Of Inertia Of A Cone
• Moment Of Inertia Of A Square
• Moment Of Inertia Of Semicircle
• Moment Of Inertia Of Solid Cone

Parallel Axis Theorem