Moment Of Inertia Of A Solid Cylinder - Formulas And Derivation

Moment of inertia of a solid cylinder about its centre is given by the formula;

\begin{array}{l} I = \frac{1}{2} M R^{2} \end{array}

Here, M = total mass and R = radius of the cylinder.

Derivation Of Moment Of Inertia Of Solid Cylinder

We will take a solid cylinder with mass M, radius R and length L. We will calculate its moment of inertia about the central axis.

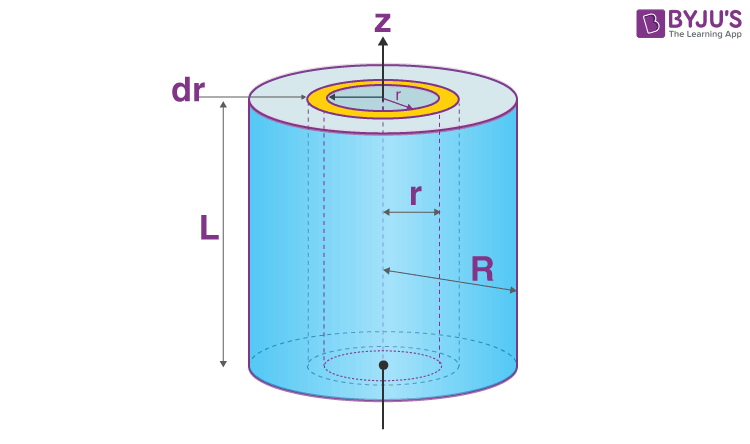
Moment Of Inertia Of Solid Cylinder

Here we have to consider a few things:

The solid cylinder has to be cut or split into infinitesimally thin rings.
Each ring consists of the thickness of dr with length L.
We have to sum up the moments of infinitesimally these thin cylindrical shells.

We will follow the given steps.

1. We will use the general equation of moment of inertia:

dI = r² dm

Now we move on to finding the dm. It is normally given as;

dm = ρ dV

In order to obtain dm we have to calculate dv first. It is given as;

dV = dA L

Meanwhile, dA is the area of the big ring (radius: r + dr) minus the smaller ring (radius: r). Hence;

\begin{array}{l} d A = π (r + d r)^{2} - π r^{2} \end{array}

\begin{array}{l} d A = π (r^{2} + 2 r d r + (d r)^{2}) - π r^{2} \end{array}

Notably, here the (dr)² = 0.

\begin{array}{l} d A = 2 π r d r \end{array}

2. Substitution of dA into dV we get;

\begin{array}{l} d V = d A L = 2 π r d r L \end{array}

Now, we substitute dV into dm and we will have;

dm = (2πrdr)Lρ

The dm expression is further substituted into the dI equation and we get;

\begin{array}{l} d I = \int r^{2} (2 π r d r) L ρ \end{array}

\begin{array}{l} I = 2 π L ρ \int_{0}^{R} r^{3} d r \end{array}

\begin{array}{l} I = 2 π L ρ [r^{4} / 4]_{0}^{R} \end{array}

\begin{array}{l} I = 2 π L ρ [R^{4} / 4] \end{array}

3. Alternatively, we have to find the expression for density as well. We use the equation;

\begin{array}{l} ρ = \frac{M}{V} \end{array}

Now,

\begin{array}{l} ρ = \frac{M}{π R^{2} L} \end{array}

4. The final step involves using integration to find the moment of inertia of the solid cylinder. The integration basically takes the form of a polynomial integral form.

\begin{array}{l} I = 2 π L \frac{M}{π R^{2} L} [R^{4} / 4] \end{array}

I = 2MR²/4

Therefore,

\begin{array}{l} I = \frac{1}{2} M R^{2} \end{array}

⇒ Check Other Object’s Moment of Inertia:

Parallel Axis Theorem

24,500

Comments

Leave a Comment Cancel reply