Moment of inertia of an annular disc that is uniform and having mass (m), thickness (t), inner radius (R₁) and outer radius (R₂) is expressed as;

Here, we have to consider that the disc is rotating about an axis passing through the centre.

Derivation Of Moment Of Inertia Of Annular Disc

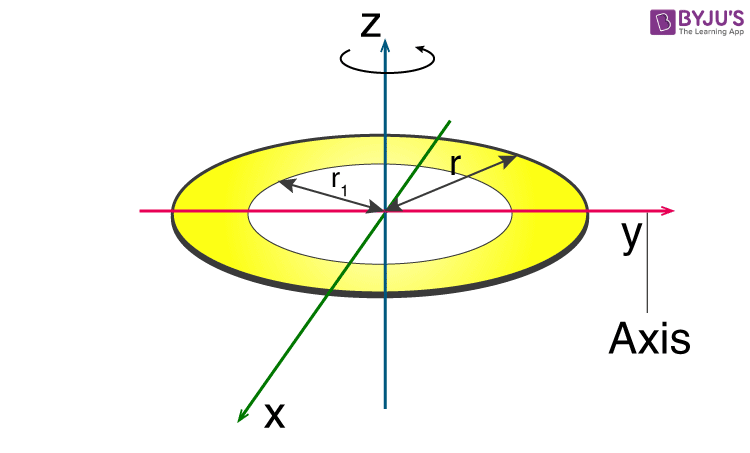
1. We will start by recalling the moment of inertia expression which is given as;

dI = r² dm

In this, we can consider dm as the mass of volume dV. We will then first consider the moment of inertia about the z-axis and we get the expression;

I_zz = _O∫^R r²dm

Like the relation in a disc, the mass dm of the volume element dV is related to volume and density by;

dm = ρ dV

We then have to calculate dV. Here we will assume that the disc will have a uniform density. Here we will also consider a ring to be at radius r with width dr and thickness t. We will get;

dV = (2 π r dr)t

If we substitute the values for dm we get;

dm = ρ (2 πt ) r dr

2. We can then write a new expression for I_zz. It will be;

I_zz = _R1∫^R2 r²dm

I_zz = 2 π ρ t _R1∫^R2 r³dr

Now we integrate between R₁ and R₂. We will now have;

I_zz = 2 π  ρ t [R₂⁴/4 – R₁⁴ / 4]

I_zz = (½) π ρ t [ R₂⁴ – R₁⁴] ……………(Equation 1)

However, we can also express it as [ R₂² + R₁²][ R₂² – R₁²]. Hence, the equation now becomes;

I_zz = ½ πρt [ R₂² + R₁²][ R₂² – R₁²] ……………..(Equation 2)

3. Now we need to find the total mass of the annular disk. We will consider the total mass (M₂) of a disc of radius R₂ and subtract it from the mass (M₁) of a disc of radius R₁.

Mass = Density x Area x Thickness

We will get,

M₂ = π ρ t R₂²

M₁ = π ρ t R₁²

So the mass of the annular disc is given as;

M_a = M₂ – M₁

M_a = π ρ t R₂² – πpt R₁²

M_a = π ρ t (R₂² – R₁²)

4. In the next step, we will substitute the above values in equation 2, which is.

I_zz = ½ π ρ t [ R₂² + R₁²][ R₂² – R₁²]

Once the values are added and after integration, we can now write the expression for moment of inertia of an annular disc as;

I_zz = ½ M_a (R₂² + R₁²)

⇒ Check Other Object’s Moment of Inertia:

• Moment Of Inertia Of A Disc
• Moment Of Inertia Of Circle
• Moment Of Inertia Of A Sphere
• Moment Of Inertia Of Triangle
• Moment Of Inertia Of Rod

Parallel Axis theorem