An angle smaller than the right angle is called an acute angle. In other words, the angle which is less than 90 degrees forms an acute angle. The polygons such as triangle, parallelogram, trapezoid, etc. consist of at least one acute angle. Let us learn here some basics of angles.
Table of Contents:
- Definition
- Degree
- Images
- Formula
- Examples
- Acute Angle Triangle
- Properties of Acute Triangle
- Acute Angle Parallelogram
- Acute Angle Trapezoid
- Applications
- Acute angle vs Obtuse angle
- FAQs
The two lines or line segments or rays with a common point leads to the formation of an angle. An angle is denoted through a symbol ‘∠’. An angle is measured with the help of a protractor in degrees (o).
- Vertex: A corner or a point where lines meet is called the vertex of an angle.
- Arms: The two lines that meet to make an angle are called arms of an angle.

- Measuring Angle: Angles can be measured using a protractor.
- Place the center of the protractor at a fixed point, say O of the angle at one of the arms.
- Another arm indicates the degree of the angle while measured from the initial hand in an anti-clockwise manner.
Acute Angle Definition
An angle which is measuring less than 90 degrees is called an acute angle. This angle is smaller than the right angle (which is equal to 90 degrees). For example, ∠30o, ∠45o, ∠60o, ∠75o, ∠33o, ∠55o, ∠85o, etc. are all acute angles. Let us see some examples here to understand.
Example: See the figure below:
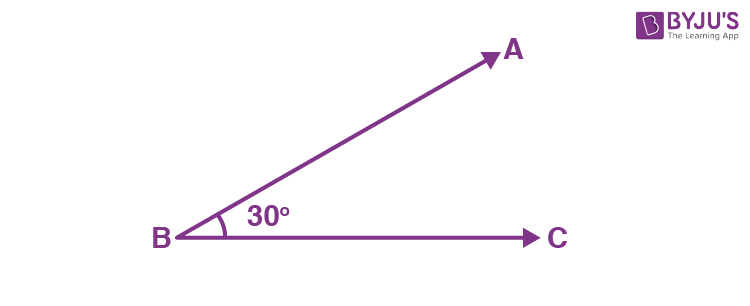
∠ABC measures 30 degrees, which is less than 90 degrees and hence it is an acute angle.
The basic types of angles are right angle, obtuse angle, acute angle.

From the above figure, we can differentiate between the three angles. The first figure shows an acute angle measuring 62 degrees (less than 90 degrees), the second figure shows a right angle measuring 90 degrees and the third figure shows an obtuse angle measuring 135 degrees (more than 90 degrees).
Note: Dividing the right angle gives us two or more acute angles since each angle formed, there will be much less than 90˚.

Also, read:
Acute Angle Degree
The degree of an acute angle measures less than 90 degrees, i.e. less than a right angle. The examples of acute angle degrees are 12°, 35°, 48°, 65°, 80°, 89°. Hence, the acute angle degree ranges from 0 degrees and less than 90 degrees.
Acute angle Images
The below figure shows the images of acute angles measuring 40 and 60 degrees.

Can two acute angles form a linear pair?
No, since the measure of a linear pair of angles should be 180 degrees and the measure of an acute angle is less than 90 degrees. Therefore, two acute angles will not form a linear pair. For example, 85° and 75° are two angles such that 85° + 75° = 160° < 180°. Thus, 85° and 75° do not form a linear pair.
Acute Angle Formula
In an acute triangle, the following statement holds good for the length of the sides:
a2 + b2 > c2
b2 + c2 > a2
c2 + a2 > b2
Where a, b and c are the sides of a triangle.
Acute Angle Examples
Example 1:
Angle A measures x degrees. Is A acute if x = 15°? If x = 65°? If x = 90°? If x = 135°?
Answer:
When x = 15°:
15 < 90
Yes, ∠A is acute angle.
When x = 65°:
65 < 90
Yes, ∠A is acute angle.
When x= 90°
90 < 90 (not true)
Alternatively, 90 = 90
So, ∠A is not acute if x = 90°.
When x = 135°:
135 < 90 (not true since 135 > 90)
So, ∠A is not acute if x = 135°.
Example 2:
Which angle is right? Acute? Obtuse?

Answer: Angle A is acute, angle B is right, and angle C is obtuse.
Acute Angle Triangle
If all the internal angles of a triangle are less than 90 degrees, then it is called an acute angle triangle.

In the above figure, we can see, the three angles of the triangle are 69°, 85° and 26°. All three angles are less than 90 degrees.
Properties of Acute Triangles
- All equilateral triangles are acute triangles. An equilateral triangle has three sides of the same length and three angles of the equal measure, i.e. 60°
- Opposite the highest angle is the longest side of an acute triangle
- Acute triangles can be isosceles, equilateral, or scalene
Acute Angle Parallelogram
A parallelogram is a quadrilateral with opposite sides being parallel and congruent (of the same length). The angles that are opposite to each other are congruent (of equal measure). A parallelogram has two acute angles and two obtuse angles. Therefore, the acute and obtuse angles should have equal measurement.

Acute Angle Trapezoid
A trapezoid is a parallelogram with one pair of opposite sides being parallel. An acute trapezoid has both interior angles (created by the base and legs which are longer) measuring less than 90°.
Example: There are two acute and two obtuse angles in the trapezoid given below.

Acute Angles in Real Life
- The angle made in letter V is an acute angle.
- If we slice a pizza into four or more slices, each slice of pizza will make an acute angle.
- The hands of a wall clock make acute angles at several hours of a day. Example, at 1 o’clock.
- The road signs, namely “One Way” and “No Left Turn” arrows show an acute angle.
- The turn signal indicator of the dashboard and the speedometer both establish acute angles inside the vehicle.
Acute Angle vs Obtuse Angle
There are some differences between acute angles and obtuse angles in terms of definition, measure and properties. Some of the major differences between acute and obtuse angles are tabulated below:
| Acute angle | Obtuse angle |
| The measure of an angle which is less than 90 degrees (right angle) is called acute angle. | The measure of an angle which is greater than 90 degrees (right angle) and less than 180 degrees is called obtuse angle. |
| Measure: Always < 90° | Measure: Between 90° and 180° |
| A triangle can have more than one acute angle. | A triangle cannot have more than one obtuse angle. |
| It’s measure is less than a right angle. | It’s measure is greater than right angle and less than straight angle. |
Frequently Asked Questions on Acute Angle – FAQs
What are the 5 types of angles?
Acute angles (< 90°) Right angles (= 90°) Obtuse angles (> 90°)
Straight angles (= 180°)
Reflex angles (> 180°)
There is another angle called full angle, which measures 360 degrees and is called a full rotation of the axis.

Comments