Before going into a representation of the decimal expansion of rational numbers, let us understand what rational numbers are. Any number that can be represented in the form of p/q, such that p and q are integers and q ≠ 0 are known as rational numbers. So when these numbers have been simplified further, they result in decimals. Let us learn how to expand such decimals here.
Examples: 6 , -8.1, 4/5 etc., are all examples of rational numbers.
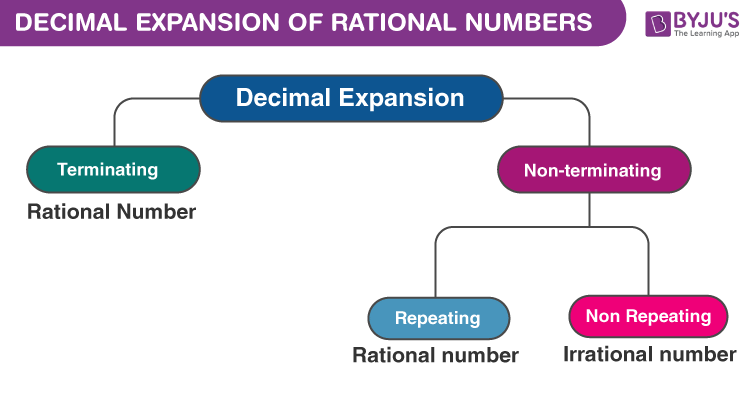
How to Expand Rational Numbers in Decimals?
The real numbers which are recurring or terminating in nature are generally rational numbers.

For example, consider the number 33.33333……. It is a rational number as it can be represented in the form of 100/3. It can be seen that the decimal part .333…… is the non-terminating repeating part, i .e. it is a recurring decimal number.
Also the terminating decimals such as 0.375, 0.6 etc. which satisfy the condition of being rational
Consider any decimal number. For e.g. 0.567. It can be written as 567/1000 or 567/103 . Similarly, the numbers 0.6689,0.032 and .45 can be written as 6689/104, 32/103, 45/102, respectively in fractional form.
Thus, it can be seen that any decimal number can be represented as a fraction which has denominator in powers of 10. We know that prime factors of 10 are 2 and 5, it can be concluded that any decimal rational number can be easily represented in the form of p/q, such that p and q are integers and the prime factorization of q is of the form 2x5y , where x and y are non-negative integers.
This statement gives rise to a very important theorem.
Theorems
Theorem 1: If m be any rational number whose decimal expansion is terminating in nature, then m can be expressed in form of p/q, where p and q are co-primes and the prime factorization of q is of the form 2x5y, where x and y are non-negative integers.
The converse of this theorem is also true and it can be stated as follows:
Theorem 2: If m is a rational number, which can be represented as the ratio of two integers i.e. p/q and the prime factorization of q takes the form 2x5y, where x and y are non-negative integers then, then it can be said that m has a decimal expansion which is terminating.
Consider the following examples:
- \(\begin{array}{l}\frac{7}{8} = \frac{7}{2^3} = \frac{7\times 5^3}{2^3\times 5^3} = \frac{875}{10^3}\end{array} \)
- \(\begin{array}{l}\frac{3}{80} = \frac{3}{2^4\times 5}= \frac{3\times 5^3}{2^4\times 5^4} = \frac{375}{10^4}\end{array} \)
Moving on, to decimal expansion of rational numbers which are recurring, the following theorem can be stated:
Theorem 3: If m is a rational number, which can be represented as the ratio of two integers i.e. p/q and the prime factorization of q does not takes the form 2x5y, where x and y are non-negative integers. Then, it can be said that m has a decimal expansion which is non-terminating repeating (recurring).
Consider the following examples:
- \(\begin{array}{l}\frac{1}{6}= 0.1666….= 0.1\overline{6}\end{array} \)
- \(\begin{array}{l}\frac{7}{12}= 0.58333…= 0.58\overline{3} \end{array} \)
- \(\begin{array}{l}\frac{9}{11}= 0.8181…= 0.\overline{81}\end{array} \)
Rational Number to decimal Examples
Case 1: Remainder equal to zero
Example: Find the decimal expansion of 3/6.

Here, the quotient is 0.5 and the remainder is 0. Rational number 3/6 results in a terminating decimal.
Case 2: Remainder not equal to zero
Example: Express 5/13 in decimal form.

Here, the quotient is 0.384615384 and the remainder is not zero. Notice that the number…384 after the decimal is repeating. Hence, 5/13 gives us a non-terminating recurring decimal expansion. And this can be written as
A rational number gives either terminating or non-terminating recurring decimal expansion. Thus, we can say that a number whose decimal expansion is terminating or non-terminating recurring is rational.
Video Lesson on Rational Numbers

Find the joy in learning with us. To know more about rational numbers please visit our website www.byjus.com and download BYJU’S-The Learning App from Google play store to learn anytime anywhere.

Please give me worksheets questions of terminating ,
Non-terminating