In coordinate geometry, Euclidean distance is defined as the distance between two points. To find the distance between two points, the length of the line segment that connects the two points should be measured. In this article, we will learn the definition of Euclidean distance, formula, derivation and examples in detail.
Table of Contents:
What is Euclidean Distance?
In Mathematics, the Euclidean distance is defined as the distance between two points. In other words, the Euclidean distance between two points in the Euclidean space is defined as the length of the line segment between two points. As the Euclidean distance can be found by using the coordinate points and the Pythagoras theorem, it is occasionally called the Pythagorean distance.
Euclidean Distance Formula
As discussed above, the Euclidean distance formula helps to find the distance of a line segment. Let us assume two points, such as (x1, y1) and (x2, y2) in the two-dimensional coordinate plane.
Thus, the Euclidean distance formula is given by:
d =√[(x2 – x1)2 + (y2 – y1)2]
Where,
“d” is the Euclidean distance
(x1, y1) is the coordinate of the first point
(x2, y2) is the coordinate of the second point.
Euclidean Distance Formula Derivation
To derive the formula for Euclidean distance, let us consider two points, say P(x1, y2) and Q(x2, y2) and d is the distance between the two points. Now, join the points P and Q using a line. To derive the Euclidean distance formula, let us construct a right triangle, whose hypotenuse is PQ. Now, draw the horizontal line and vertical line from P and Q which meet at the point R as shown in the figure given below.
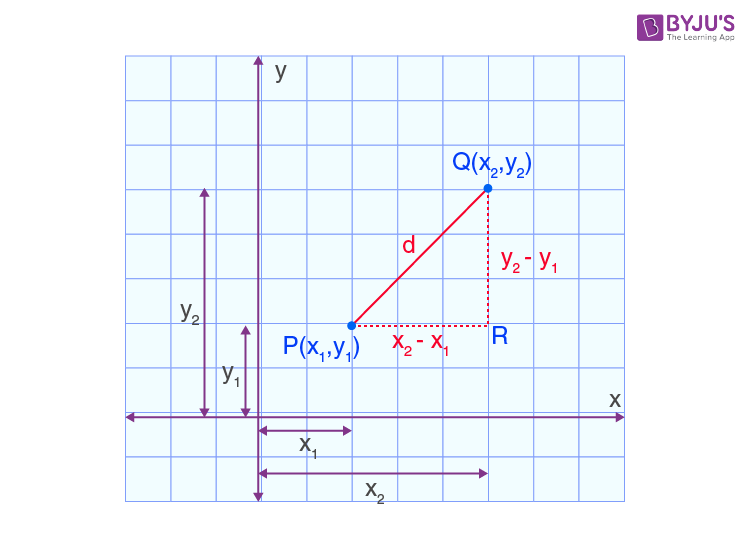
Now, we have to apply Pythagoras theorem to the triangle PQR to find the distance between two points.
Using Pythagoras theorem,
Hypotenuse2 = Base2 + Perpendicular2
PQ2 = PR2 + QR2
Therefore, d2 = (x2 – x1)2 + (y2 – y1)2
Now, take square root on both sides of equation, we get
d =√[(x2 – x1)2 + (y2 – y1)2]
Hence, the formula for Euclidean distance is derived.
|
Also, read: |
Euclidean Distance Examples
Example 1:
Determine the Euclidean distance between two points (a, b) and (-a, -b).
Solution:
Let the point P be (a, b) and Q be (-a, -b)
i.e. P(a, b) = (x1, y1) and Q(-a, -b) = (x2, y2)
We know that the Euclidean distance formula is,
Euclidean distance, d = √[(x2 – x1)2 + (y2 – y1)2]
Now, substitute the values in the formula, we get
d = √[(-a – a)2 + (-b – b)2]
d = √[(-2a)2 + (-2b)2]
d = √[4a2 + 4b2]
d = √4(a2+b2)
d = 2√(a2+b2).
Hence, the distance between two points (a, b) and (-a, -b) is 2√(a2+b2).
Example 2:
Find the distance between two points P(0, 4) and Q(6, 2).
Solution:
Given:
P(0, 4) = (x1, y1)
Q(6, 2) = (x2, y2)
The distance between the point PQ is
PQ = √[(x2 – x1)2 + (y2 – y1)2]
PQ = √[(6 – 0)2 + (2 – 4)2]
PQ = √[(6)2 + (-2)2]
PQ = √(36+4)
PQ = √40
PQ = 2√10.
Therefore, the distance between two points P(0,4) and Q(6, 2) is 2√10.
Practice Question on Euclidean Distance
- Find the Euclidean distance between the points (2, 3) and (4, 1).
- Find the distance between the points (6, 2) and (9, 1).
- Determine the Euclidean distance between the points (3, 4) and (6, 7).
To learn more Maths-related concepts, stay tuned with BYJU’S – The Learning App and download the app today!
Frequently Asked Questions on Euclidean Distance
What is Euclidean distance?
In Mathematics, the Euclidean distance is the distance between two points or the straight line distance.
What is the formula for Euclidean distance in the two dimensional plane?
If (x1, y1) and (x2, y2) are the two points in the two-dimensional plane, the Euclidean distance formula is given by:
Euclidean distance, d = √[(x2 – x1)2 + (y2 – y1)2]
Does the Pythagoras theorem help to find the Euclidean distance?
Yes, the Pythagoras theorem helps to find the Euclidean distance.
Can we find the Euclidean distance for a three-dimensional plane?
Yes, we can find the Euclidean distance for a three-dimensional plane.
When can we use the Euclidean distance formula?
The Euclidean distance formula helps to find the length of the line segment, which helps to prove the given vertices form the square, rectangle, triangle and so on.
Comments