In the expansion of a binomial term (a + b) raised to the power of n, we can write the general and middle terms based on the value of n. Before getting into the general and middle terms in binomial expansion, let us recall some basic facts about binomial theorem and expansion.

Here, the coefficients nCr are called binomial coefficients. There will be (n+1) terms in the expansion of (a+b)n , i.e., one more than the index. Also, in the successive terms of the expansion, we can observe that the index of “a” decreases by unity. It is n in the first term, (n – 1) in the second term, and so on, ending with zero in the last term. At the same time, the index of “b” increases by unity, starting with zero in the first term, 1 in the second, and so on ending with n in the last term.
General Term of the Binomial Expansion
Consider the expansion of the binomial term (a + b) rained to the power n, i.e. the binomial expansion of (a + b)n:

Here,
First term = nC0 an
Second term = nC1 an–1b
Third term = nC2 an–2b2
…..
(r + 1)th term = nCr an–rbr
From the above pattern of the successive terms, we can say that the (r + 1)th term is also called the general term of the expansion (a + b)n and is denoted by Tr+1.

This formula is used to find the specific terms, such as the term independent of x or y in the binomial expansions of (x + y)n. Go through the example given below to understand how the general term formula of binomial expansion helps.
Example 1:
Find y if the 17th and 18th terms of the expansion (2 + y)50 are equal.
Solution:
(r + 1)th term of the expansion of (a + b)n = Tr+1 = nCr an-r br
Here, a = 2, b = y, n = 50
17th term = (16 + 1)th term, i.e. r = 16
T17 = T16+1 = 50C16 (2)50-16 y16
= 50C16 (2)34 (y)16
Similarly, 18th term = (17 + 1)th term, i.e. r = 17
T18 = T17+1 = 50C17 (2)50-17 y17
= 50C13 (2)33 (y)17
According to the given,
T17 = T18
50C16 (2)34 (y)16 = 50C13 (2)33 (y)17
⇒ y = (2 × 50C16)/50C17
= 2 × [50!/(16! 34!)] × [(17! 33!)/50!]
= 2 × [(17 × 16! × 33!)/ (16! × 34 × 33!)]
= 1
Therefore, y = 1
| Read more: |
|---|
Middle Term of the Binomial Expansion
As we know, the expansion of (a + b)n contains (n + 1) number of terms. Based on the value of n, we can write the middle term or terms of (a + b)n.
That means, if n is even, there will be only one middle term and if n is odd, there will be two middle terms.
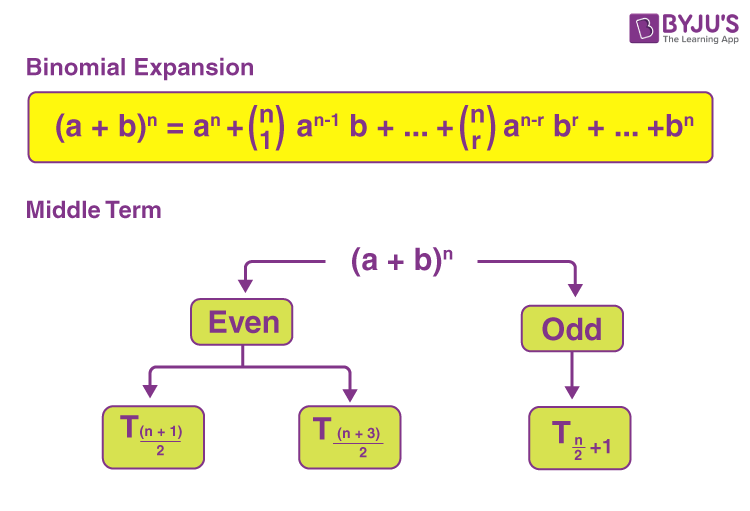
When n is Even
If n is even, then the number of terms in the expansion will be n + 1. Since n is even so n + 1 is odd. Therefore, the
When n is Odd
If n is odd, then n +1 is even, there will be two middle terms in the expansion, and they are:
and
Thus,
Let’s have a look at the examples given below to learn how to find the middle terms in the binomial expansions.
Example 2:
Find the middle term(s) in the expansion of (x + 2y)9.
Solution:
Given: (x + 2y)9
Comparing with (a + b)n, we get;
a + x, b = 2y and n = 9 (odd)
As the value of n is odd, there will be two middle terms.
(n + 1)/2 = (9 + 1)/2 = 10/2 = 5
(n + 3)/2 = (9 + 3)/2 = 12/2 = 6
Thus, 5th and 6th terms are the middle terms.
T5 = T4+1 = 9C4 (x)9-4 (2y)4 {since Tr+1 = nCr an-r br}
= 126 x5 (2)4 (y)4
= (126 × 16) x5 y4
= 2016 x5 y4
Also, T6 = T5+1 = 9C5 (x)9-5 (2y)5
= 126 x4 (2)5 (y)5
= (126 × 32) x4 y5
= 4032 x4 y5
Therefore, 2016 x5 y4 and 4032 x4 y5 are the middle terms in the expansion of (x + 2y)9.
Example 3:
Find the middle term(s) in the expansion of (x + 3)8.
Solution:
Given: (x + 3)8
Comparing with (a + b)n, we get;
a + x, b = 3 and n = 8 (even)
So, there will be only one middle term.
(n/2) + 1 = (8/2) + 1 = 4 + 1 = 5
Thus, 5th term is the middle term.
T5 = T4+1 = 8C4 (x)8-4 (3)4 {since Tr+1 = nCr an-r br}
= 70 x4 × 81
= (70 × 81) x4
= 5670 x4
Hence, 5670 x4 is the middle term of the expansion (x + 3)8.
Practice Problems
Try solving the following questions for better understanding of the concepts.
1. Find the coefficient of x5y7 in the expansion of 9x – 2y)12.
2. Find the 8th term in the expansion of (2x – y)11.
3. Show that the coefficient of the middle term in the expansion of (1 + x)2n is equal to the sum of the coefficients of two middle terms in the expansion of (1 + x)2n – 1.
4. Find the middle terms in the expansions of (12 – x3)7.
For more interesting maths concepts, visit byjus.com and download BYJU’S – The Learning App for engaging videos to learn the concepts effectively.

Comments