Heron’s Formula Class 9 Notes: Chapter 12

According to the CBSE Syllabus 2023-24, this chapter has been renumbered as Chapter 10.

CBSE Class 9 Maths Heron’s Formula Notes – Download PDF Here

In geometry, a triangle is a closed three-dimensional figure. In this article, you are going to learn Heron’s formula for class 9, which is used to find the area of triangles. You will also learn how Heron’s formula is used to find the area of other polygons in detail.

Triangle

  The plane closed figure, with three sides and three angles is called as a triangle.

Types of triangles:
Based on sides –  a) Equilateral b) Isosceles c) Scalene
Based on angles – a) Acute-angled triangle b) Right-angled triangle c) Obtuse-angled triangle

For more information on Triangles, watch the below video

To know more about Triangles and Its Type, visit here.

Area of a Triangle

$Area=$$(1/2)\; \times base\times height$

In the case of equilateral and isosceles triangles, if the lengths of the sides of triangles are given, we use Pythagoras’ theorem in order to find the height of a triangle.

To know more about the Area of a triangle, visit here.

Area of an Equilateral Triangle

Consider an equilateral $\Delta ABC$, with each side as $a$ unit. Let AO be the perpendicular bisector of BC. In order to derive the formula for the area of an equilateral triangle, we need to find height AO.

Using Pythagoras’ theorem,
$A{C}^2=O{A}^2+O{C}^2$
$O{A}^2=A{C}^2-O{C}^2$
Substitute $AC=a,O\mathrm{C\; =\; a/2\; in\; the\; above\; equation.}$
$O{A}^2=a^2-$$a^2$/4
$OA=$√3a/2

We know that the area of the triangle is:
$A=$$(1/2)\; \times base\times height$
$A=$$(1/2)\; \times a\times \; (\surd 3a/2)$

$\therefore AreaofEquilateraltriangle= \surd 3a2$/4

Area of an Isosceles Triangle

Consider an isosceles $\Delta ABC$ with equal sides as $a$ units and base as $b$ units.

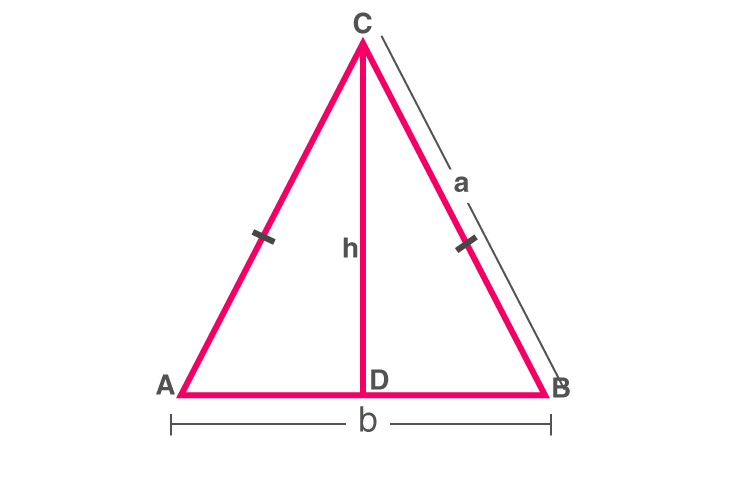
Isosceles triangle ABC

The height of the triangle can be found by Pythagoras’ Theorem :
$C{D}^2=A{C}^2-A{D}^2$
$\Rightarrow \mathrm{h2}=a^2-\; (b2$/4) = (4$a^2$– $b2$)/4

$\Rightarrow h=$$\sqrt{$ a^2$$ b2$}$
Area of triangle is $A=$$\mathrm{(1/2)b}h$
$\therefore A=$$(1/2)\; \times b\times$$\sqrt{$ \sqrt{$ a^2$$ b2$}$}$

$\therefore A=$$(1/4)\; \times b\times \surd (4a2 – b2)$

Area of a Triangle – By Heron’s formula

Area of a $\Delta ABC$, given sides a, b, c  by Heron’s formula (also known as Hero’s Formula) is:

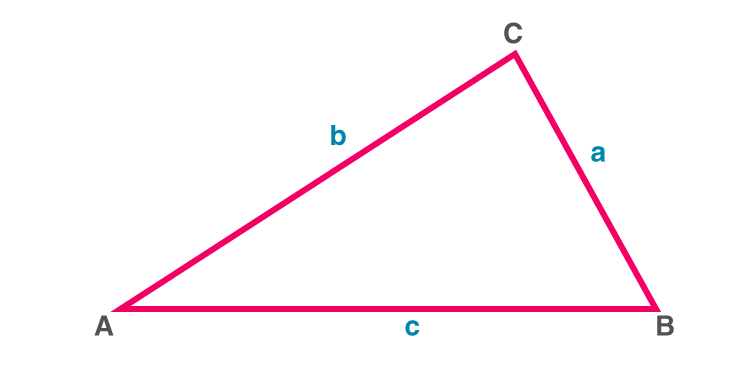
Triangle ABC

Find semi perimeter (s) $=$(a + b + c)/2

$Area= \surd [s(s\; –\; a)(s\; –\; b)(s\; –\; c)]$

This formula is helpful in finding the area of a scalene triangle, given the lengths of all its sides.

To know more about Heron’s Formula, visit here.

Area of Any Polygon – By Heron’s formula

For a quadrilateral, when one of its diagonal values and the sides are given, the area can be calculated by splitting the given quadrilateral into two triangles and using Heron’s formula.

Example: A park, in the shape of a quadrilateral ABCD, has $\angle C={90}^{\circ },$ AB = 9 cm, BC = 12 cm, CD = 5 cm and AD = 8 cm. How much area does it occupy?

$\Rightarrow$We draw the figure according to the information given.

The figure can be split into 2 triangles $\Delta BCDand\Delta ABD$
From $\Delta BCD$, we can find BD (Using Pythagoras’ Theorem)
$B{D}^2={12}^2+5^2=169$
$BD=13cm$
Semi-perimeter for $\Delta BCD{S}_1=$(12 + 5 + 13)/2 = 15

Semi-perimeter $\Delta ABD{S}_2=$(9 + 8 + 13)/2 = 15

Using Heron’s formula $A_{1}and{A}_2$$will\; be:$

$A1 = \surd [15(15\; –\; 12)(15\; –\; 5)(15\; –\; 13)]$

$A1 = \surd (15\; \times \; 3\; \times \; 10\; \times \; 2\; )$
$A_1=\surd 900\; =30c{m}^2$
Similarly,

$A_2$ will be $35.49c{m}^2.$
The area of the quadrilateral $ABCD=A_1+A_2=65.49c{m}^2$