Intermediate Value Theorem

The intermediate value theorem is a theorem about continuous functions. Intermediate value theorem has its importance in Mathematics, especially in functional analysis. This theorem explains the virtues of continuity of a function. The two important cases of this theorem are widely used in Mathematics. Let us go ahead and learn about the intermediate value theorem and its two statements in this article.

Intermediate Value Theorem Statement

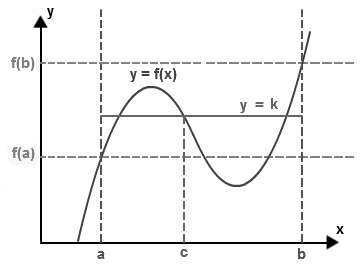
Intermediate value theorem states that if “f” be a continuous function over a closed interval [a, b] with its domain having values f(a) and f(b) at the endpoints of the interval, then the function takes any value between the values f(a) and f(b) at a point inside the interval. This theorem is explained in two different ways:

Statement 1:

If k is a value between f(a) and f(b), i.e.

either f(a) < k < f(b) or f(a) > k > f(b)

then there exists at least a number c within a to b i.e. c ∈ (a, b) in such a way that f(c) = k

Statement 2:

The set of images of function in interval [a, b], containing [f(a), f(b)] or [f(b), f(a)], i.e.

either f([a, b]) ⊇ [f(a), f(b)] or f([a, b]) ⊇ [f(b), f(a)]

Theorem Explanation:

The statement of intermediate value theorem seems to be complicated. But it can be understood in simpler words. Let us consider the above diagram, there is a continuous function f with endpoints a and b, then the height of the point “a” and “b” would be “f(a)” and “f(b)”.

If we pick a height k between these heights f(a) and f(b), then according to this theorem, this line must intersect the function f at some point (say c), and this point must lie between a and b.

An intermediate value theorem, if c = 0, then it is referred to as Bolzano’s theorem.

Intermediate Theorem Proof

We are going to prove the first case of the first statement of the intermediate value theorem since the proof of the second one is similar.

We will prove this theorem by the use of completeness property of real numbers. The proof of “f(a) < k < f(b)” is given below:

Let us assume that A is the set of all the values of x in the interval [a, b], in such a way that f(x) ≤ k.

Here A is supposed to be a non-empty set as it has an element “a” and also A is bounded above by the value “b”.

Thus, by completeness property, we have that, “c” be the lowest value which is greater than or equal to each element of A. Hence, we can say that f(c) = k.

Given that f is continuous. Then let us consider a ε > 0, there exists “a δ > 0” such that

| f(x) – f(c) | < ε for every | x – c | < δ. This gives us

f(x) – ε < f(c) < f(x) + ε

For each x lying within c – δ and c + δ. So, we have values of x lying between c and c -δ, contained in A, such that :

f(c) < (f(x) + ε) ≤ (k + ε) ——– (1)

Similarly, values of x between c and c + δ that are not contained in A, such that

f(c) > (f(x) – ε) > (k − ε) ——–(2)

Combining both the inequality relations, obtain

k – ε < f(c) < k + ε

For every ε > 0

Hence, the theorem is proved.

Intermediate Theorem Applications

The intermediate value theorem has many applications. Mathematically, it is used in many areas. This theorem is utilized to prove that there exists a point below or above a given particular line. It is also used to analyze the continuity of a function that is continuous or not.

This theorem has many implications in Physics and Chemistry problems too. It is applicable whenever there is a continuously varying scalar quantity with endpoints sharing the same value for a variable. These quantities may be – pressure, temperature, elevation, carbon dioxide gas concentration, etc.

Intermediate value theorem has some significant real-life applications too. Let us take an example of a wobbly table due to the uneven ground. In order to fix this, rotate the table, provided that the ground is continuous; i.e. no ups and downs due to poorly-fitted tiles.

The wobbly table will have three of its legs touching the ground, while its fourth leg will be the problem. While rotating the table at a point, the fourth leg will be below the ground, and at some other point, it will lie above the ground. According to the intermediate value theorem, there will be a point at which the fourth leg will perfectly touch the ground, and the table is fixed.

Intermediate Theorem Example

Question:

Check whether there is a solution to the equation x⁵ – 2x³ -2 = 0 between the interval [0, 2].

Solution:

Let us find the values of the given function at the x = 0 and x = 2.

f(x) = x⁵ – 2x³ -2 = 0

Substitute x = 0 in the given function

f(0) = (0)⁵ – 2(0)³ -2

f(0) = -2

Substitute x = 2 in the given function

f(2) = (2)⁵ – 2(2)³ -2

f(2) = 32 – 16 – 2

f(2) = 14

Therefore, we conclude that at x = 0, the curve is below zero; while at x = 2, it is above zero.

Since the given equation is a polynomial, its graph will be continuous.

Thus, applying the intermediate value theorem, we can say that the graph must cross at some point between (0, 2).

Hence, there exists a solution to the equation x⁵ – 2x³ -2 = 0 between the interval [0, 2].

Visit BYJU’s – The Learning App and download the app to explore all the important Maths-related videos to learn with ease.