Laws of Vector Addition
A vector is a physical quantity which is represented both in direction and magnitude. In the upcoming discussion, we shall learn about how to add different vectors. There are different laws of vector addition and they are:
- Triangle law of vector addition
- Parallelogram law of vector addition
Triangle Law of Vector Addition:
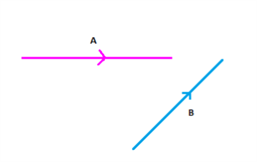
Suppose, we have two vectors A and B as shown.
 Now the method to add these is very simple, what we do is to simply place the head of one vector over the tail of the other vector as shown below.
Now the method to add these is very simple, what we do is to simply place the head of one vector over the tail of the other vector as shown below.
 Now join the other endpoints of both the vectors together as shown in the below figure.
Now join the other endpoints of both the vectors together as shown in the below figure.
 The resultant of the given vectors is given by the vector C which represents the sum of vectors A and B.
The resultant of the given vectors is given by the vector C which represents the sum of vectors A and B.
i.e. C = A + B
Vector addition is commutative in nature i.e.
if C = A + B; then C = B + A
Or
A + B = C = B + A
Similarly, if you want to subtract both the vectors using the triangle law then simply reverse the direction of any vector and add it to the other one as shown.
 Now, this can be represented mathematically as:
Now, this can be represented mathematically as:
C = A – B
Parallelogram Law of Vector Addition:
This law is also very similar to the triangle law of vector addition. Consider the two vectors again.
 Now for using the parallelogram law, we represent both the vectors as adjacent sides of a parallelogram and then the diagonal emanating from the common point represents the sum or the resultant of the two vectors and the direction of the diagonal gives the direction of the resultant vector.
Now for using the parallelogram law, we represent both the vectors as adjacent sides of a parallelogram and then the diagonal emanating from the common point represents the sum or the resultant of the two vectors and the direction of the diagonal gives the direction of the resultant vector.
 The resultant vector is shown by C. This is known as the parallelogram law of vector addition.
The resultant vector is shown by C. This is known as the parallelogram law of vector addition.
By using the orthogonal system of vector representation the sum of two vectors
a = \(\begin{array}{l}a_1 \hat{i} + a_2 \hat{j} + a_3 \hat{k}\end{array} \)
and b = \(\begin{array}{l}b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k}\end{array} \)
is given by adding the components of the three axes separately.
i.e. a + b = \(\begin{array}{l}a_i \hat{i} + a_2 \hat{j} + a_3 \hat{k} + b_1 \hat{i} + b_2 \hat{j} + b_3 \hat{k} \end{array} \)
\(\begin{array}{l}\Rightarrow a + b \end{array} \)
= \(\begin{array}{l}(a_1 +b_1)\hat{i} + (a_2 + b_2)\hat{j} + (a_3 + b_3)\hat{k} \end{array} \)
Similarly, the difference can be given as \(\begin{array}{l}a – b\end{array} \)
= \(\begin{array}{l}(a_1 – b_1)\hat{i} + (a_2 – b_2)\hat{j} + (a_3 – b_3) \hat{k}\end{array} \)
Now let us take an example to understand this topic better.
Example: Let \(\begin{array}{l}\overrightarrow{a}\end{array} \)
=\(\begin{array}{l} 3\hat{i} + 4\hat{j} – 7\hat{k}\end{array} \)
and \(\begin{array}{l}\overrightarrow{b}\end{array} \)
=\(\begin{array}{l} 6\hat{i} + 4\hat{j} – 6\hat{k}\end{array} \)
. Add both the vectors.
Solution: As both the vectors are already expressed in co-ordinate system we can directly add these as follows
\(\begin{array}{l}\overrightarrow {a} + \overrightarrow{b}\end{array} \)
=\(\begin{array}{l} (3 + 6)\hat{i} + (4 + 4)\hat{j} + (-7 – 6)\hat{k}\end{array} \)
or \(\begin{array}{l}\overrightarrow{a} + \overrightarrow{b}\end{array} \)
=\(\begin{array}{l} 9\hat{i} + 8\hat{j} -13\hat{k}\end{array} \)
Thus, you are now thorough with how vectors are added and subtracted. There are other operations like vector multiplication which are very important in terms of understanding vectors better. To practice more on vectors with laws of vector addition, download BYJU’S – The learning app.






Comments