Components Of A Vector

The components of a vector in two dimension coordinate system are usually considered to be x-component and y-component. It can be represented as, V = (v_x, v_y), where V is the vector. These are the parts of vectors generated along the axes. In this article, we will be finding the components of any given vector using formula both for two-dimension and three-dimension coordinate system.

Components of a Vector Definition

Suppose a vector V is defined in a two-dimensional plane. The vector V is broken into two components such as v_x and v_y

Now let an angle θ, is formed between the vector V and x-component of vector. The vector V and its x-component (v_x) form a right-angled triangle if we draw a line parallel to y-component (v_y).

By trigonometric ratios, we know,

cos θ = Adjacent Side/Hypotenuse = v_x/V

sin θ = Opposite Side/Hypotenuse = v_y/V

where V is the magnitude of the vector V.

Components of vector formula

Since, in the previous section we have derived the expression:

cos θ = v_x/V

sin θ = v_y/V

Therefore, the formula to find the components of any given vector becomes:

v_x=V cos θ

v_y=Vsin θ

Where V is the magnitude of vector V and can be found using Pythagoras theorem;

|V| = √(v_x², v_y²)

Orthogonal vectors

Vectors can be easily represented using the co-ordinate system in three dimensions. Before getting into the representation of vectors, let us understand what orthogonal representation is.

In terms of coordinate geometry, by orthogonal representation, we mean parameters that are at right angles to each other. In orthogonal three dimensional system, we have three axes perpendicular to each other, which represent x,y and z axis.

Unit vectors: are the vectors which have magnitude of unit length.

Here,

In orthonormal or orthogonal systems, we can have three different unit vectors with one in each direction. It can be represented as follows:

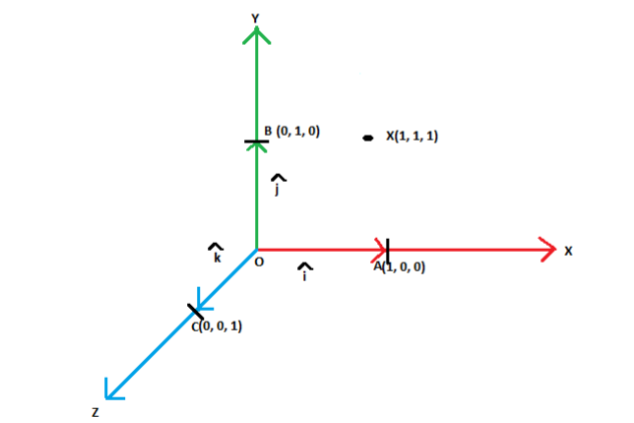
The point X(1, 1, 1) can be represented using the three mutually perpendicular axes as points A(1, 0, 0), B(0, 1, 0) and C(0, 0, 1)  on the and axes respectively.

The magnitude of the vector

Now, with the help of unit vectors we can represent any vector in the three-dimensional coordinate system.

Components of vector in 3D

To represent a vector in space, we resolve the vector along the three mutually perpendicular axes as shown below.

The vector OM can be resolved along the three axes as shown. With OM as the diagonal, a parallelepiped is constructed whose edges OA, OB and OC lie along the three perpendicular axes.

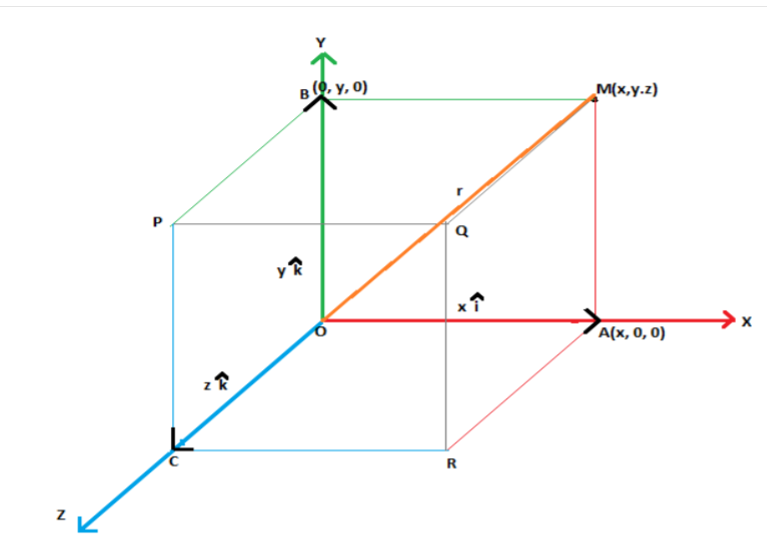
From the above figure, we can say that

The vector can be represented as

This is known as the component form of a vector.

Thus, the vector r can be resolved in the directions i, j and k respectively. This represents the position of given vectors in terms of the three co-ordinate axes.

If a vector is given in a form as shown above, then the magnitude of such a vector can be found out by using the Pythagoras theorem in the given figure as ,

r =

The sum of two vectors a =

i.e.a + b =

Similarly, the difference can be given as:

a – b =

We can perform a number of mathematical operations on vectors using this system of representation. It is both easy and simple. To make our understanding more clear, let us take an example.

Vector Components Problem

Example: Two vectors are given by a =

Solution: The unit vector is given by

The magnitude of both the vectors can be given as:

|a| =

|b| =

Now, the unit vectors can be given as:

The sum can be given by:

a + b =

a + b =

The difference is given by:

a – b =