Odd Function

A function f is said to be an odd function if -f(x) = f(-x), for all value of x. In Mathematics, the functions even and odd are those that satisfy specific symmetry relations, with respect to considering additive inverses. They are fundamental in the analysis of mathematics, power and the Fourier series. They are called for the parity (property of an integer of either being even or odd) of the powers pertaining to the power functions that hold good for each condition: the function f (x) = xⁿ belongs to the even function category if n is an integer that is even else the function is odd if n being an odd integer.

What is an Odd Function?

Assume f to be a real-valued function of a variable that is real. The function f is odd when the equation is valid for all the values of x in a way that x and – x is present in the domain of the function f,

-f(x) = f(-x)

Or equivalently,

f(x) + f(-x) = 0

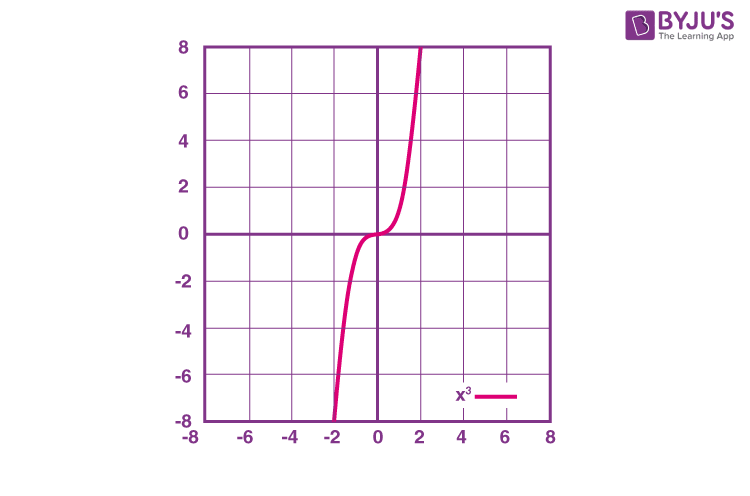
For example, f(x) = x³ is an odd function, because for all value of x, -f(x) = f(-x).

Graph of Odd Function

The graph of an odd function consists of symmetry that is rotational with respect to the origin that means that the graph remains unchanged post the 180-degree rotation about the origin.

Properties of Odd Function

• Uniqueness
  • If the given function is even and odd together, it is equal to zero at every point defined.
  • If the given function is odd, the absolute value of the function is even in nature.
• Addition and subtraction
  • The sum total of any two odd functions is also odd.
  • The difference between any two odd functions is also odd.
• Multiplication and division
  • The product of any two odd functions is an even function.
  • The quotient of any 2 odd functions is an even function.
• Composition: The composition of any 2 odd functions is odd.
• The derivative of any given odd function is even in nature.
• The integral of any given odd function from the limits – A to + A is 0.
  \(\begin{array}{l}{\displaystyle \int _{-A}^{A}f(x)\,dx=0}\end{array} \)
• The Maclaurin series of any given odd function consists of odd powers only.

Odd Function Formula

The formula for the odd function is given by the reflection:

-f(x) = f(-x),  for all value of x.

where f(x) is any function.

Let us solve some examples based on this formula.

Related Articles

• Real functions
• Identity function
• Taylor Series

Odd Function Solved Examples

Example 1: Is the function f (x) = -3x³ + 2x an odd or even function?

Answer:

The given function is said to be odd if – f (x) = f (- x).

f(x) = -3x³ + 2x

f(-x) = -3(-x)³ + 2(-x)

= -3(-1)³ x³ + 2(-x)

= 3x³ – 2x      ………(i)

-f(x) = – (-3x³ + 2x)

= 3x³ – 2x     ……….(ii)

From (i) and (ii), we get;

f (- x) = – f (x).

The given function is an odd function.

Example 2: Is the function f (x) = x³ + 2x an odd or even function?

Answer:

The given function is termed

• even if f (x) = f (- x)
• odd if f (- x) = – f (x)

f(-x) = (-x)³ + 2(-x)

= -x³ – 2x

= – (x³ + 2x)

= – f(x)

f (- x) = – f (x) implies an odd function.

Odd Function and Even Function

As we have already discussed, an odd function f(x) satisfies the statement, f(-x) = -f(x), for all x.

A function f is said to be an even function, if;

f(x) = f(-x), for all value of x.

Equivalently,

f(x) – f(-x) = 0

For example, f(x) = x² is an even function.