Functions are one of the very important concepts in mathematics which have got numerous applications in the real world. Be it the mega skyscrapers or the superfast cars, their modelling requires methodical application of functions. Almost all the real-world problems are formulated interpreted and solved using real functions.
What are Functions and Relations?
A relation is a rule that “relates” an element from one set to an element from another set. A function is a special kind of relation. A relation F is said to be a function if each element in set A is associated with exactly one element in set B., For example, a relation F from set A to set B such that it associates a natural number to its square is a function because for every element in set A, we will have exactly one association in set B.
Operations on Real Functions
Now that we understand what functions are let us discuss how we perform mathematical operations on real functions such as the addition of two or more functions, subtraction of two functions, multiplying a real function by a real number etc.
Adding Two Real Functions
For adding two real functions let us define the functions f and g such that f: X ⟶R and g: X ⟶R are two real functions such that X is a subset of R. Then (f + g): X ⟶R can be defined as:
(f + g)(x)=f(x) + g(x), for all x ϵ X
Subtracting Two Functions
For subtracting two real functions let us define the functions f and g such that f: X ⟶R and g: X ⟶R are two real functions such that X is a subset of R. Then (f – g): X ⟶R can be defined as:
(f – g)(x)=f(x) – g(x), for all x ϵ X
Multiplying a Real Function by a Scalar (Real Number)
Let us define a real function f such that f: X ⟶R, X⊆R and a ϒ be a real scalar quantity. Then the product of scalar ϒ and the function f is also a function defined from X to R as:
(ϒf)(x) = ϒf(x), for all x ϵ X
Multiplying Two Functions
For multiplying two real functions let us define the functions f and g such that f: X ⟶R and g: X ⟶R are two real functions such that X is a subset of R. Then fg: X ⟶R can be defined as:
(fg)(x) = f(x)g(x), for all x ϵ X
Quotient of Two Functions
For determining the quotient of two real functions let us define the functions f and g such that f: X ⟶R and g: X ⟶R are two real functions such that X is a subset of R. Then f/g: X ⟶R can be defined as: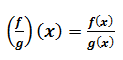
Given that g (x) ≠ 0, for all x ɛ X
Recommended Videos
Relations and Types of Relations
Functions – Introduction, Co-domain and Range
Functions and Types of Functions
Range of Functions – Concepts & Questions
Learn more NCERT solutions for Relations and Functions.
Comments