Perimeter of Rectangle Questions

The perimeter of rectangle questions and answers are available to help students comprehend the many kinds of the perimeter of rectangle questions. The perimeter of a shape, as we all know, is its outer boundary. To help you comprehend the concept fast, we’ve offered a variety of perimeter of rectangle questions with clear solutions. To understand more about the perimeter of a rectangle, click here.

Perimeter of Rectangle Questions with Solutions

1. Determine the perimeter of a rectangle whose length is 12 cm and breadth is 8 cm.

Solution:

Using the perimeter of a rectangle formula, we can easily find the rectangle’s perimeter.

As we know,

Perimeter of rectangle = 2(length + breadth) units.

Given that, Length = 12 cm, and breadth = 8 cm.

Now, substitute the values in the perimeter formula, we get

Perimeter of rectangle = 2(12 + 8)

Perimeter = 2(12 + 8)

Perimeter = 2 × 20

Perimeter = 40 cm.

Therefore, the perimeter of the rectangle is 40 cm.

2. A bedsheet has a length of 120 inches and a breadth of 95 inches. How much lace will be required to complete the border?

Solution:

The perimeter of the bed sheet will be determined using the perimeter of the rectangle formula in order to determine the amount of lace required for the bedsheet’s border.

Given,

Length, l = 120 inches

Breadth, b = 95 inches.

As we know, the perimeter of a rectangle = 2(l + b) units.

Substituting the values in the formula, we get

Perimeter = 2(120 + 95) = 2 × 215 = 430 inches.

Hence, we will need 430 inches of lace to complete the border.

3. Determine the rectangle’s perimeters whose length equals 5 cm, and breadth equals 3 cm.

Solution:

Given that, Length, l = 5 cm

Breadth, b = 3 cm

The formula to calculate the perimeter of a rectangle is given as follows:

Perimeter = 2 × (Length + Breadth) units.

Now, substitute the values in the formula, we get

Perimeter = 2 × (5 + 3) cm

Perimeter = 2 (8) cm

Perimeter = 16 cm

So, the perimeter of the rectangle is equal to 16 cm.

4. The length of the rectangular field is 90 m, and its perimeter is 240 m. Calculate the breadth of the rectangular field.

Solution:

Given: Perimeter = 240 m and length, l = 90 m.

To find: Breadth (b).

As we know, rectangle’s perimeter = 2 (l + b)

Using the given values, we can derive the following:

2(l + b) = 240 m

Now, bring 2 to the right side of the equation,

Hence, we get

l + b = 120 m

Now, substitute l = 90 m

90+ b = 120 m

On simplifying the above equation, we get

b = 120 – 90 m

b = 30 m

Hence, the breadth of the rectangular field is 30 m.

5. Find the breadth of a rectangular plot, if its area is 440 m² and the length is 22 m. Also, find its perimeter.

Solution:

Given: Area of rectangular plot = 440 m².

Length = 22 m.

To find: Breadth and perimeter of the rectangular plot.

As we know,

Area = Length × Breadth

Now, substitute the values in the formula to find the breadth.

440 = 22 × Breadth

Hence, Breadth = 440/22 = 20 m

Therefore, the breadth of the rectangular plot = 20 m.

Now, substitute the length and breadth values in the perimeter formula,

Perimeter = 2 (Length + Breadth) units

Perimeter = 2 (22 + 20)

Perimeter = 2 (42)

Perimeter = 84 m

Therefore, the perimeter of the rectangular plot of land is 84 m.

Also, read: Rectangle.

6. Find the perimeter of a rectangle for the figure given below:

Solution:

From the given figure, it is observed that,

Length = 30 cm and breadth = 20 cm.

Now, put the values in the perimeter of rectangle formula, we get

Perimeter of rectangle = 2 × (length + breadth) units

Perimeter = 2 × (30 + 20)

Perimeter = 2 × 50

Perimeter = 100 cm

Therefore, the perimeter of the rectangle, if length = 30 cm and breadth = 20 cm, is 100 cm.

7. A rectangle’s perimeter is 40 metres. Its length is 4 metres shorter than five times its breadth. Calculate the rectangle’s area.

Solution:

Given: Perimeter of rectangle = 40 m.

Assume that the rectangle’s breadth is x.

According to the given condition, then the rectangle’s length will be 5x−4.

As we know, perimeter of rectangle = 2(length + breadth) units

Now, substitute the obtained values in the formula,

⇒ 40 = 2(5x−4+x)

On simplifying the above equation,

⇒ 40 = 2 (6x- 4)

⇒ 40 = 12x- 8

⇒ 12x = 40+8

⇒ 12x = 48

⇒ x = 48/12

​⇒ x = 4

Therefore, the breadth of the rectangle = 4 m.

So, Length = 5(4) – 4

Length = 20 – 4

Length = 16

Hence, the length of the rectangle = 16 m.

We know that,

Area of rectangle = length × breadth square units.

Area = 16 × 4 m²

Area = 64 m²

Hence, the area of the rectangle is 64 m².

8. As illustrated in the diagram below, rectangle MNOP is composed of 4 congruent rectangles. Determine the perimeter of MNOP if one of the rectangles has an area of 8 m² and a breadth of 2 m.

Solution:

Now, name the given figure as follows:

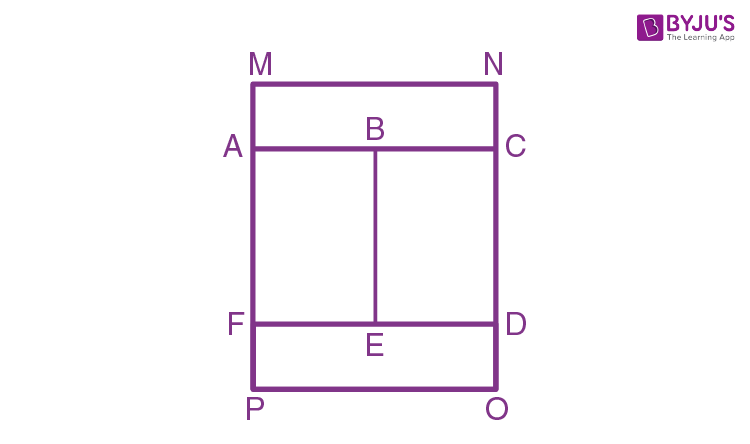
Given that, the area of one rectangle is 8m²

Also, breadth = 2m

As we know, Area = length × breadth

Now, substitute the values in the formula,

⇒ length × breadth = 8

⇒ length × 2 = 8

⇒ length = 4 m

Since all the four rectangles are congruent, all the rectangles have a length 4 m and a breadth 2m.

Now, perimeter of rectangle MNOP is determined as follows:

= MN + NC + CD + DO + PO + PF + FA + MA

Here, small lengths represent the breadth, while longer lengths represent the length.

Therefore, perimeter of rectangle MNOP = 4 + 2 + 4 + 2 + 4 + 2 + 4 + 2 = 24m

Thus, the perimeter of the rectangle MNOP is 24 metres.

9. A rectangle with a perimeter of 264 cm is split into 5 congruent rectangles, as shown in the figure below. Find one of the rectangles’ perimeter.

Solution:

Given that rectangle’s perimeter = 264 cm.

Also, The rectangle is split into 5 congruent rectangles.

To find: Perimeter of one rectangle.

Now, name the figure as shown below with the letters “l” and “b”.

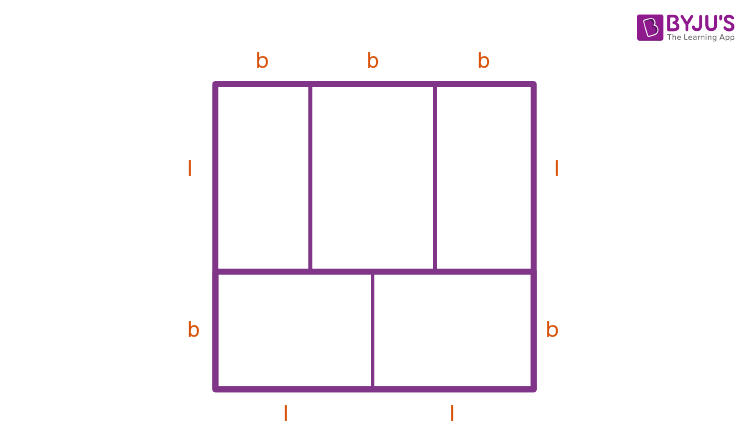
Assume that, length = l and breadth = b

As we know, rectangle’s perimeter = 2(length + breadth) units

From the diagram as shown above, the perimeter of a rectangle is calculated as follows:

= l + b + l + l + b + l + b + b + b

= 4l + 5b

Therefore, 264 = 4l + 5b … (1)

In addition, the figure shows that the 3 breadth of the top vertical rectangles is equal to the 2 lengths of the 2 bottom horizontal rectangles.

Hence, we can write,

2l = 3b … (2)

Now, substitute (2) in (1),

264 = 2(3b) + 5b

On simplifying the above equation, we get

264 = 6b + 5b

11b = 264

b = 264/11

b = 24 cm

Hence, breadth = 24 m

Now, put b = 24 in (2)

Therefore, we get

2l = 3(24)

l = 3(24)/2

l = 3(12)

l = 36 cm

Hence, length = 36 cm

Therefore, the perimeter of one rectangle = 2(36 + 24)

= 2(60)

= 120 cm

Therefore, one of the rectangles’ perimeter is 120 cm.

10. For her remote control car, Aashika created a miniature oval race circuit. The illustration below shows her concept. How far around the track is the whole distance? To the nearest whole centimetre, round your answer.

Solution:

The perimeter of the given track = Total distance around the track

The track is made up of two semi-circular paths and a rectangular path.

Therefore, the perimeter of the given track = 52 + 52 + 2πr

Perimeter = 52 + 52 + [2(22/7)16]

Perimeter = 104+100.57

Perimeter = 204.57 ≈ 205 cm.

Hence, the total distance around the track rounded to the nearest whole centimetre is 205 cm.

Explore More Articles:

• Rectangle Questions
• Circle Questions
• Geometry Questions
• Area of Parallelogram Questions
• Series Questions

Practice Questions

1. Determine the length and perimeter of a rectangle whose area is 96 cm² and breadth is 8 cm.
2. Compute the perimeter of a rectangle, given that the area of a rectangle is 240 sq. cm and the length is 20 cm.
3. Find the perimeter of a rectangle whose length, l = 5 cm and b = 4 cm.