CBSE Class 10 Maths Notes Polynomial:-Download PDF Here
Class 10 Maths Chapter 2 Polynomial Notes
CBSE Class 10 Maths Chapter 2 Polynomial Notes are provided here in detail. Here, we are going to discuss the complete explanation of what is polynomial and its types, algebraic expressions, degree of a polynomial expression, graphical representation of the polynomial equations, factorization, relationship between zeroes and coefficient of a polynomial, and so on with many examples.
Students can refer to the short notes and MCQ questions along with separate solution pdf of this chapter for quick revision from the links below:
Algebraic Expressions
An algebraic expression is an expression made up of variables and constants along with mathematical operators.
An algebraic expression is a sum of terms, which are considered to be building blocks for expressions.
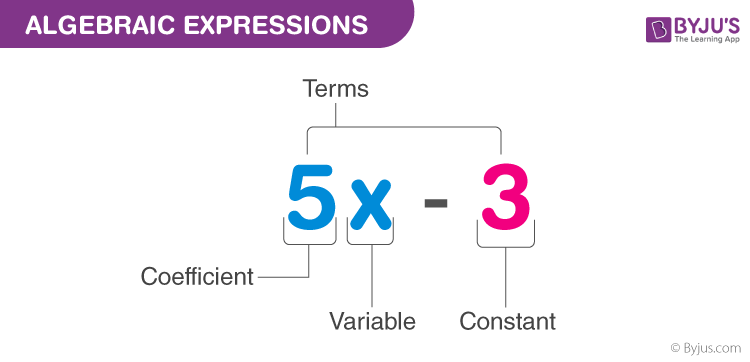
A term is a product of variables and constants. A term can be an algebraic expression in itself.
Examples of a term – 3, which is just a constant.
– 2x, which is the product of constant ‘2’ and the variable ‘x’
– 4xy, which is the product of the constant ‘4’ and the variables ‘x’ and ‘y’.
– 5x2y, which is the product of 5, x, x and y.
The constant in each term is referred to as the coefficient.
Example of an algebraic expression: 3x2y+4xy+5x+6 which is the sum of four terms: 3x2y, 4xy, 5x and 6.
An algebraic expression can have any number of terms. The coefficient in each term can be any real number. There can be any number of variables in an algebraic expression. The exponent on the variables, however, must be rational numbers.
To know more about Algebraic Expressions, visit here.
Polynomial
An algebraic expression can have exponents that are rational numbers. However, a polynomial is an algebraic expression in which the exponent on any variable is a whole number.
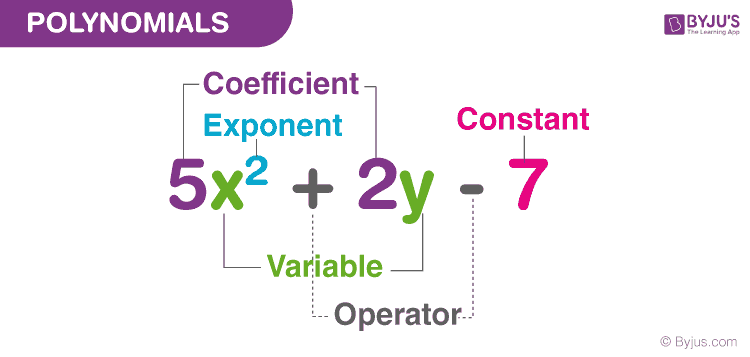
Let us consider a few more examples,
5x3+3x+1 is an example of a polynomial. It is an algebraic expression as well.
2x+3√x is an algebraic expression but not a polynomial. – since the exponent on x is 1/2, which is not a whole number.
To know more about polynomials, visit here.
Degree of a Polynomial
For a polynomial in one variable – the highest exponent on the variable in a polynomial is the degree of the polynomial.
Example: The degree of the polynomial x2+2x+3 is 2, as the highest power of x in the given expression is x2.
Consider another example, the degree of the polynomial x8 + 2x6 – 3x + 9 is 8 since the greatest power in the given expression is 8.
Types Of Polynomials
Polynomials can be classified based on the following.
a) Number of terms
b) Degree of the polynomial.
Types of Polynomials Based on the Number of Terms
a) Monomial – A polynomial with just one term. Example: 2x, 6x2, 9xy
b) Binomial – A polynomial with two unlike terms. Example: 4x2+x, 5x+4
a) Trinomial – A polynomial with three unlike terms. Example: x2+3x+4
Types of Polynomials based on Degree
Linear Polynomial
A polynomial whose degree is one is called a linear polynomial.
For example, 2x+1 is a linear polynomial.
Quadratic Polynomial
A polynomial of degree two is called a quadratic polynomial.
For example, 3x2+8x+5 is a quadratic polynomial.
To know more about the types of polynomials, click here.
For more information on Quadratic Polynomials, watch the below video

Cubic Polynomial
A polynomial of degree three is called a cubic polynomial.
For example, 2x3+5x2+9x+15 is a cubic polynomial.
Graphical Representations
Let us learn here how to represent polynomial equations on the graph.
Representing Equations on a Graph
Any equation can be represented as a graph on the Cartesian plane, where each point on the graph represents the x and y coordinates of the point that satisfies the equation. An equation can be seen as a constraint placed on the x and y coordinates of a point, and any point that satisfies that constraint will lie on the curve.
For example, the equation y = x, on a graph, will be a straight line that joins all the points which have their x coordinate equal to their y coordinate. Example – (1,1), (2,2) and so on.
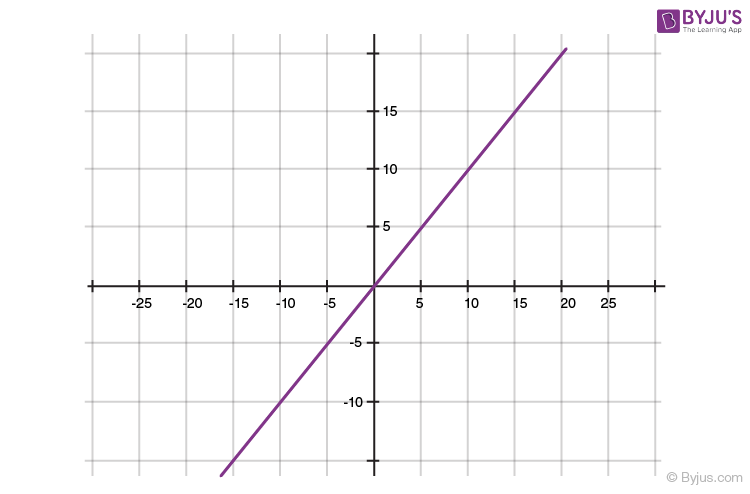
Geometrical Representation of a Linear Polynomial
The graph of a linear polynomial is a straight line. It cuts the X-axis at exactly one point.
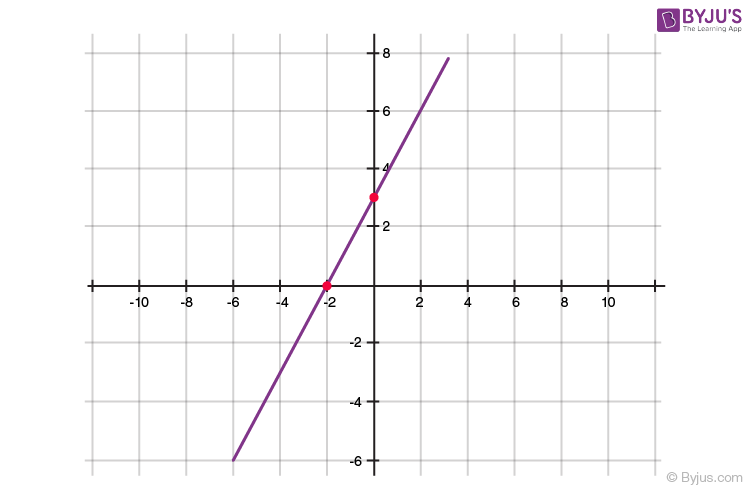
Geometrical Representation of a Quadratic Polynomial
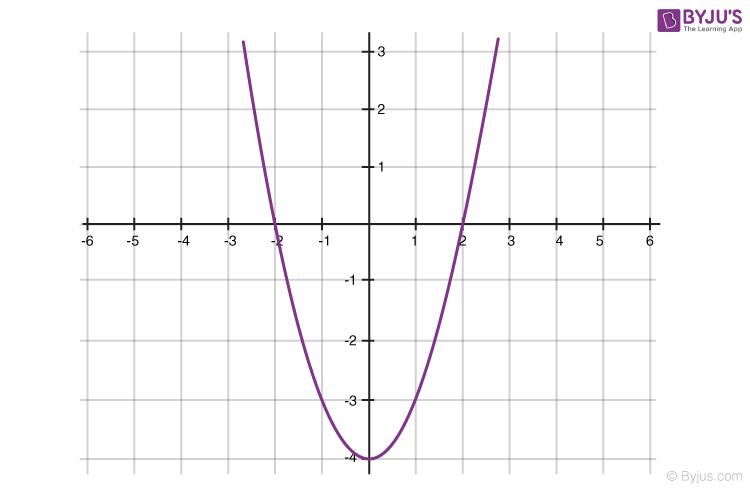


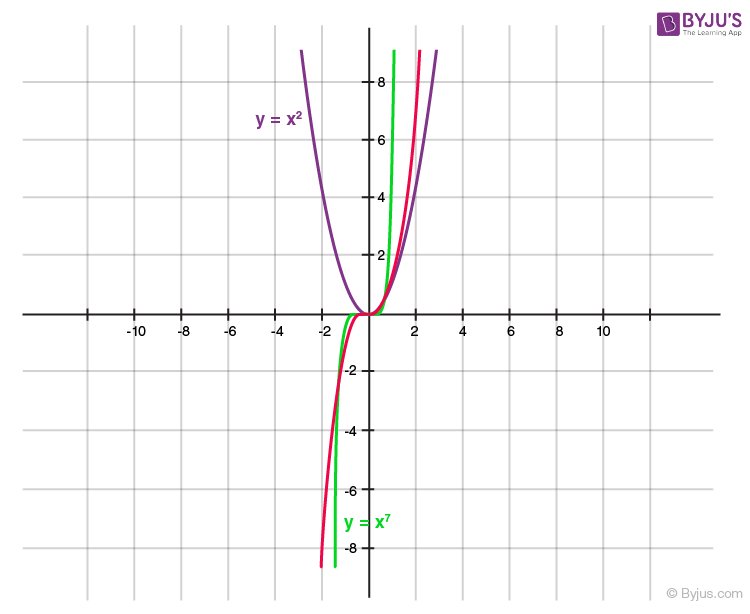
Graph of the Polynomial x^n
For a polynomial of the form y=xn where n is a whole number:
Zeroes of a Polynomial
A zero of a polynomial p(x) is the value of x for which the value of p(x) is 0. If k is a zero of p(x), then p(k)=0.
For example, consider a polynomial p(x)=x2−3x+2.
When x=1, the value of p(x) will be equal to
p(1)=12−3×1+2
=1−3+2
=0
Since p(x)=0 at x=1, we say that 1 is a zero of the polynomial x2−3x+2
Video Lesson on Zeroes of Polynomials

To know more about Zeroes of a Polynomial, visit here.
Geometrical Meaning of Zeros of a Polynomial
Geometrically, zeros of a polynomial are the points where its graph cuts the x-axis.
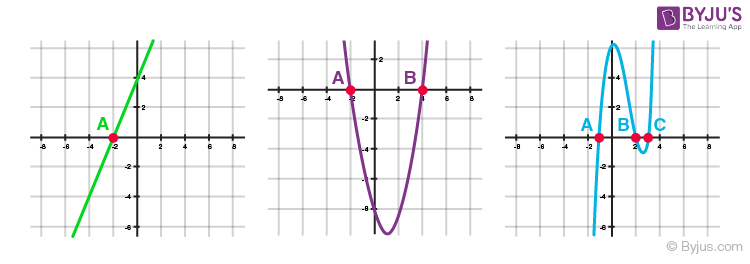
Here A, B and C correspond to the zeros of the polynomial represented by the graphs.
Number of Zeros
In general, a polynomial of degree n has at most n zeros.
- A linear polynomial has one zero,
- A quadratic polynomial has at most two zeros.
- A cubic polynomial has at most 3 zeros.
Factorisation of Polynomials
Quadratic polynomials can be factorized by splitting the middle term.
For example, consider the polynomial 2x2−5x+3
Splitting the middle term:
The middle term in the polynomial 2x2−5x+3 is -5x. This must be expressed as a sum of two terms such that the product of their coefficients is equal to the product of 2 and 3 (coefficient of x2 and the constant term)
−5 can be expressed as (−2)+(−3), as −2×−3=6=2×3
Thus, 2x2−5x+3=2x2−2x−3x+3
Now, identify the common factors in individual groups
2x2−2x−3x+3=2x(x−1)−3(x−1)
Taking (x−1) as the common factor, this can be expressed as:
2x(x−1)−3(x−1)=(x−1)(2x−3)
For more information on Factorisation Of Quadratic Polynomials, watch the below video

To know more about Factorisation of Polynomials, visit here.
Relationship between Zeroes and Coefficients of a Polynomial
For Quadratic Polynomial:
If α and β are the roots of a quadratic polynomial ax2+bx+c, then,
α + β = -b/a
Sum of zeroes = -coefficient of x /coefficient of x2
αβ = c/a
Product of zeroes = constant term / coefficient of x2
For Cubic Polynomial
If α,β and γ are the roots of a cubic polynomial ax3+bx2+cx+d, then
α+β+γ = -b/a
αβ +βγ +γα = c/a
αβγ = -d/a
Example
Calculate the sum of the zeroes and the product of the zeroes of the polynomial 9x2 – 16x + 20.
Solution:
Given polynomial: 9x2 – 16x + 20
The given polynomial is a quadratic polynomial, as the degree of the polynomial is 2.
We know that the standard form of a quadratic polynomial is ax2 + bx + c.
By comparing the given polynomial and the standard form, we can write.
a = 9
b = -16
c = 20
By using the relationship between zeroes and the coefficients of the polynomial, we can get the following:
For a quadratic polynomial,
The sum of zeroes = -coefficient of x /coefficient of x2
Now, substitute the values in the formula, we get
Sum of zeroes = -(-16)/9 = 16/9.
Similarly, Product of zeroes = constant term / coefficient of x2
Plugging the values in the above formula, we get
Product of zeroes = 20/9
Hence, 16/9 and 20/9 are the sum and the product of the zeroes of the polynomial 9x2 – 16x + 20.
To know more about Relationship between Zeroes and Coefficients of a Polynomial, visit here.
Division Algorithm
Let us assume that P(x) and G(x) are the two polynomials, such that G(x)≠ 0, then the division algorithm states the formula to find Q(x) and R(x) of the polynomial.
Here, P(x) denotes dividend polynomial
G(x) denotes divisor polynomial
Q(x) denotes quotient polynomial
R(x) denotes the remainder polynomial.
Thus, the formula stated by division algorithm is:
P(x) = G(x) × Q(x) + R(x)
To divide one polynomial by another, follow the steps given below.
Step 1: Arrange the terms of the dividend and the divisor in the decreasing order of their degrees.
Step 2: To obtain the first term of the quotient, divide the highest degree term of the dividend by the highest degree term of the divisor Then carry out the division process.
Step 3: The remainder from the previous division becomes the dividend for the next step. Repeat this process until the degree of the remainder is less than the degree of the divisor.

Algebraic Identities
1. (a+b)2=a2+2ab+b2
2. (a−b)2=a2−2ab+b2
3. (x+a)(x+b)=x2+(a+b)x+ab
4. a2−b2=(a+b)(a−b)
5. a3−b3=(a−b)(a2+ab+b2)
6. a3+b3=(a+b)(a2−ab+b2)
7. (a+b)3=a3+3a2b+3ab2+b3
8. (a−b)3=a3−3a2b+3ab2−b3
For more information on Algebraic Identities, watch the below videos


To know more about Algebraic Identities, visit here.
Polynomials for Class 10 Examples
Example 1:
Determine the quadratic polynomial, whose zeroes are 5-3√2 and 5+3√2.
Solution:
Given zeroes: 5-3√2 and 5+3√2.
Finding sum of zeroes:
Sum of zeroes = (5-3√2)+(5+3√2)
Sum of zeroes = 5+5 = 10.
Finding product of zeroes:
Product of zeroes = (5-3√2)(5+3√2)
We know that a2-b2 = (a+b)(a-b).
Hence, (5)2– (3√2)2 = (5-3√2)(5+3√2).
Therefore, product of zeroes = 25 – [9(2)]= 25 – 18 = 7
Thus, the required quadratic polynomial is:
P(x)= x2 -(sum of zeroes)x + product of zeroes
P(x) = x2-10x+7.
Hence, the required quadratic polynomial is x2-10x+7.
Example 2:
Find the zeroes of the quadratic polynomial 6x2-3-7x. Also, verify the relationship between the zeroes and the coefficient of a polynomial.
Solution:
Given quadratic polynomial: 6x2-3-7x.
Let P(x) = 6x2-3-7x.
We know that zero of a polynomial is a value of x, when P(x) = 0.
Hence, 6x2-7x-3 = 0
Now, factorize the above polynomial equation to find the value of x.
Thus, 6x2-7x – 3 = 0 is also written as:
6x2-9x+2x-3 = 0
3x(2x-3)+1(2x-3) = 0
(3x+1) (2x-3) =0
Thus, 3x+1 = 0 and 2x-3 =0
⇒3x+1 = 0
x = -1/3.
Similarly,
⇒2x-3 = 0
⇒x = 3/2.
Hence, the zeroes of the quadratic polynomial 6x2– 7x-3 are -1/3 and 3/2.
Thus, α = -1/3 and β = 3/2 are the zeroes of the polynomial.
Now, comparing P(x) = 6x2-7x-3 with ax2+bx+c.
Hence, a = 6, b=-7 and c = -3.
Verifying the Relationship Between Zeroes and Coefficient of Polynomial:
Sum of zeroes:
We know that the sum of zeroes = – coefficient of x/Coefficient of x2.
Thus, α+β = -b/a
Now, substitute the values, we get
(-1/3)+(3/2) = -(-7)/6
(-2+9)/6 = 7/6
7/6 = 7/6.
Hence, LHS = RHS.
Product of Zeroes:
We know that the product of zeroes = Constant term/Coefficient of x2.
Therefore, αβ = c/a
On substituting the values, we get
(-1/3)(3/2) = (-3/6)
-1/2 = -1/2
Hence, LHS = RHS.
Therefore, the relationship between the zeroes and coefficients of the polynomial 6x2-7x-3 is verified.
Stay tuned with BYJU’S – The Learning App and download the app to learn all class-wise concepts easily by exploring more videos.

it was very useful
This notes helped me a lot.
Very helpful and best material ever!!!!!!!!!!!1111
nice its helpful
really it will help me in board exams
I learnt a lot of formulas through these notes
it is very useful for me
it has many useful questions related to class 10 exams .
I test myself in quiz thanks a lot