In measuring angles, we generally use two types of measuring units, namely degrees and radians. Both measurements are widely used units in geometry and trigonometry in solving many problems. In general, the degree measure is used in earlier classes of mathematics since it is easy to understand and remember as this involves use of a protractor to measure the angle. In case of radians, one should understand the concept of circles and related terms along with their meaning and formulas. In this article, what is the radian measure of an angle, how to find the measure of an angle in radians and measurement of different angles in radians are explained.
Radian Measure Definition
Angle subtended at the centre by an arc of length 1 unit in a unit circle (circle of radius 1 unit) is said to have a measure of 1 radian. The symbol used to denote the radian measure is “rad” or “c”. This is shown in the figure given below.

The circumference of a circle of radius 1 unit is 2π since the circle’s circumference with radius “r” is 2πr.
Thus, one complete revolution of the initial side subtends an angle of 2π radians.
Further, in a circle of radius r, an arc of length r will subtend an angle of 1 radian.
Also, learn more about Arc here.
Radian Measure Formula
As we know, equal arcs of a circle subtend equal angles at the centre. Considering a circle.
Radius = r
Arc length = r
Angle = 1 radian
From this, we can say that an arc of length l will subtend an angle whose measure is l/r radian.
Let r be the radius of a circle, l be its arc length subtends an angle θ radian at the centre. Thus,
θ = l/r
Or
l = r θ
Radian measure of an Angle
The below figure shows the radian measure of different angles such as 1 rad, -1 rad, 1 ½ rad, and -1 ½ rad.

Radian Measure and Degree Measure
We know that the measurement of an angle can be performed in either of the measures, i.e. radian measure or degree measure. Also, we can define a relation between these two so that we can convert one unit of measurement to another, i.e. from radian measure to degree measure and vice versa.
1 radian = 180°/π = 57° 16′ (approx)
1° = π/180 radian = 0.01745329252 rad (approx)
Using the above relations, let’s convert a few angles. These are useful to learn how to find the radian measure for any given angle.
Radian Measure of 25 degrees
We know that,
1° = π/180 radian
25° = 25 × (π/180)
25° = 5π/36 rad
Or
25° = 0.13888888889π rad = 0.436332313 rad {since 1° = 0.01745329252 rad}
Radian Measure of 240 degrees
We know that,
1° = π/180 radian
240° = 240 × (π/180)
240° = 4π/3 rad
Or
240° = 1.3333333333π rad = 4.1887902048 rad {since 1° = 0.01745329252 rad}
Radian Measure of 520 degrees
We know that,
1° = π/180 radian
520° = 520 × (π/180)
520° = 26π/9 rad
Or
520° = 2.8888888889π rad = 9.0757121104 rad {since 1° = 0.01745329252 rad}
Radian measure Circle
Unlike degree measures, it is possible to represent the radian measure of an angle using a circle. The below figure shows the radian measure of some specific angles.
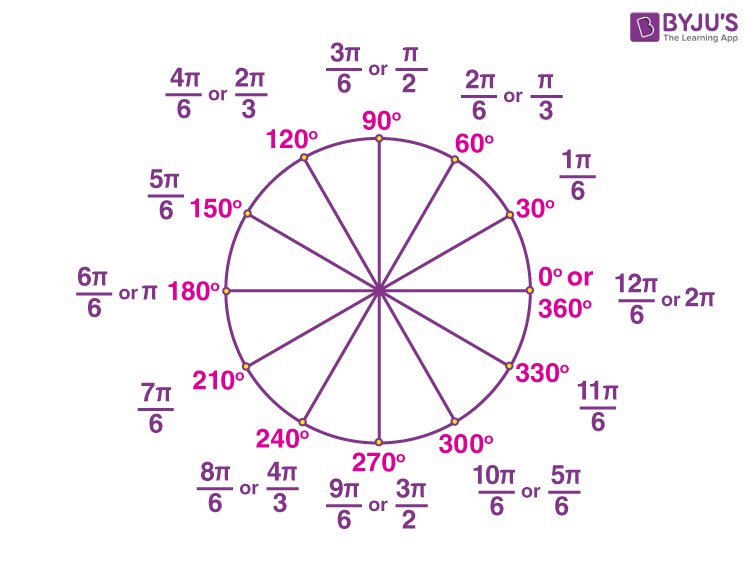
Radian Measure Examples
Go through the solved examples given below.
Example 1:
Which radian measure is equivalent to -15 degrees?
Solution:
We know that,
1° = π/180 radian
-15° = -15 × (π/180)
= -0.083333333333π rad
= -0.2617993878 rad
Therefore, -0.2617993878 rad is equivalent to -15 degrees.
Example 2:
Which radian measure is equivalent to 75 degrees?
Solution:
We know that,
1° = π/180 radian
75° = 75 × (π/180)
= 0.41666666667π rad
= 1.308996939 rad
Therefore, 1.308996939 rad is equivalent to 75 degrees.
Example 3:
How many radians is 90 degrees?
Solution:
As we know, one complete revolution = 2π radians or 360°
Thus, 360° = 2π rad
Therefore, 90° = (90°/360°) × 2π = π/2 rad
Hence, π/2 radians is 90°.

Comments