Square root of 121 is 11. It is represented as √121 = 11.
When a number is multiplied by itself the resultant number is called the square of a number. And the process of finding the number that is multiplied by itself is called finding the square root. The square root of any number is an integer. ie + or -ve. The square root of 121 is 11, as 121 is a perfect square number. √121 can be either positive or negative. i.e 11 × 11 is 121 or – 11 × – 11 is also 121. The methods of finding the square root of 121 can be determined using prime factorisation method, long division method, simplified method and repeated subtraction method.
Refer to the topic What is Square root? for more clarity.
Note the Following:
The Square root of 121 = √121 where √ = radical, and 121 is the radicand.
Exponential Form of Square root of 121 = 1211/2.
Solution for √121 = 11
Square root of 121 is Irrational = False
What is the Square root of 121?
The square root of 121 is 11. In other words, the square of 11 is 121. i.e 11 × 11 is 121.
|
√121 = 11 |
How to Find the Square root of 121?
There are three methods to find the Square root of 121:
- Prime Factorisation method
- Long Division method
- Repeated Subtraction method
Square root of 121 by Prime Factorisation Method
As 121 is a perfect square number, 121 can be divided continuously by a prime number, until the remainder becomes 1. The same prime divisors are grouped into 2 ( as this is a square root) and the groups are multiplied to get the square root.
The given number, 121 will be expressed as;
|
11 |
121 |
|
11 |
11 |
|
× |
1 |
121 = 11 × 11
Therefore the square root of 121 = 11.
Square root of 121 by Long Division Method
In the long division method, the given numbers are paired in groups, starting from the right side. Let us understand the long division method, in detailed steps;
Step 1: Grouping the given number into pairs
Given number is 121, grouping it as 1 and 21.
|
1 21 |
Step 2: Consider the first number, which is 1.
Let us find a square number that divides 7
i.e 1 × 1 = 1
2 × 2 = 4
The square number that is to be considered for dividing 1 will be 1 x 1
Step 3: Dividing 1 by 1
Step 4: Continue the division using the next number 21
The first number to be used as the next divisor is 1 × 1 = 1 (Divisor of first division + by quotient of first division)
Now considering a two digit number starting with 2 to divide 21 will be
21 × 1 = 21
Continue the division as:
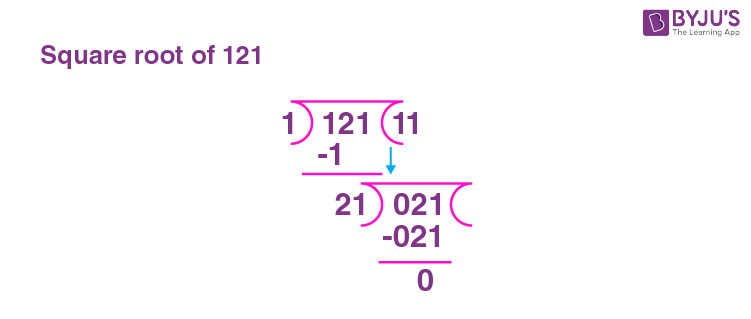
Since the Division is complete with remainder as zero, the quotient becomes the square root of the given number.
Therefore the Square root of 121 is 11.
Square root of 121 by Repeated Subtraction Method.
In the repeated subtraction method, the given number is subtracted repeatedly by odd numbers till the final solution is zero. The total number of times the subtraction is performed, becomes the square root. Please note that, if the given number is not a perfect square number, then the result 0 is not obtained.
For the given number 121, steps for repeated subtraction are
|
Step 1 |
121 |
– |
1 |
= |
120 |
|
Step 2 |
120 |
– |
3 |
= |
117 |
|
Step 3 |
117 |
– |
5 |
= |
112 |
|
Step 4 |
112 |
– |
7 |
= |
105 |
|
Step 5 |
105 |
– |
9 |
= |
96 |
|
Step 6 |
96 |
– |
11 |
= |
85 |
|
Step 7 |
85 |
– |
13 |
= |
72 |
|
Step 8 |
72 |
– |
15 |
= |
57 |
|
Step 9 |
57 |
– |
17 |
= |
40 |
|
Step 10 |
40 |
– |
19 |
= |
21 |
|
Step 11 |
21 |
– |
21 |
= |
0 |
Since the result of zero is obtained in the 11th Step, the square root of 121 is 11.
Video Lessons
Visualising square roots

Finding Square roots

Related Articles
- Square Root
- Squares and Square roots
- Finding Square roots
- 1 to 50 Square and Square root List
- Finding Square root with Example
- Square root Calculator
Solved Examples
1. Find the square root of 121 by pairing factors.
The factors of 121 are 1, 11 and 121. The pairs are
1 × 121, 11 × 11
Therefore, the square root of 121 is 11 using pairing factors 11 and 11.
2. What is the square of 11?
The square of 11 is nothing but 11 times 11 and that is 121.
Comments