Square Root of 208

The square root of 208 is irrational. The approximate value of square root of 208 is 14.4. Consider an integer “i” such that “+i × +i” = 208 or “-i × -i” = 208, then ‘i’ will be termed as the square root of 208 and 208 a perfect square number. Different methods can be used to simplify the square root of any number. A few are by prime factorisation method, long division method or repeated subtraction method. All the details on these methods are detailed in this article. 

Consider the number 15 × 15 = 225 and 14 × 14 = 196. 208 lies between 196 and 225. So the square root of 208 lies between 14 and 15, as 208 is not a perfect square number. Hence, the square root of 208 is also not a perfect integer. Therefore, √208 is an irrational number. You can refer to What is Square root?

Note the Following:

• The Square root of 208 = 2√208 = √208 where ‘√’ is the radical, and 208 is the radicand and 2 is the index.
• Exponential Form of Square root of 208 = 208^1/2
• Solution for √208 ≈ 14.42
• The square root of 208 is Irrational = True

What is the Square root of 208?

The square root of 208 is 14.4, as the square root of 208 is irrational.

How to Find the Square root of 208?

There are three methods to find the Square root of 208 

• Prime Factorisation method
• Long Division method
• Repeated Subtraction method

Square root of 208 by Prime Factorisation Method

In the prime factorization method, 208 is divided by prime factors. Starting with 2. 

The prime factors of 208 are 2, 3 and 5. 

208 = 2 × 2 × 2 × 2× 13

If we had to group the same prime numbers of two, then only 2 can be grouped into 2 groups.

√208 = √(2 × 2 × 2 × 2 × 13)

√208 = 2 × 2√(13) = 4√13

The division on 208 using prime factors is given below;

Square root of 208 by Long Division Method

To understand the long division method, follow the below mentioned detailed steps.

The number 208 is grouped as 2 and 08. Finding a square number such that 2 is divisible by a perfect square. Continue the division with the next pair. 

The first divisor in the next division to be (Divisor of first division + quotient of first division) such that

d1 × 1 =

d2 × 2 =

d3 x 3 =

And so on. 

If the division remainder is zero, then the quotient will be the square root, else the number doesn’t have a square root.

Applying the above steps to 208.

Pairing 2 and 08.

The squares are:

1 × 1 = 1

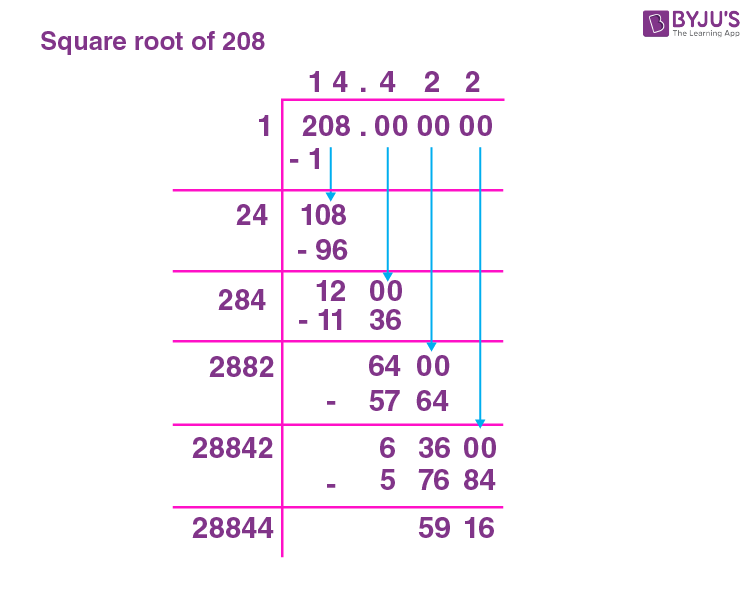
No further division is possible and the remainder is non-zero. Hence, 208 does not have a perfect square. Therefore, 208 is an irrational number which is 4√13.

Square root of 208 by Repeated Subtraction Method.

When 208 is repeatedly subtracted by odd numbers, i.e., 208 – 1 = 149. Now 149 – 3 = 146 then with 7 and so on. When this repeated subtraction results in zero at any point, 208 will be a perfect square number. If the subtraction results in a negative number, then 208 will not be a perfect square number, and hence it won’t have a square root. 

The table below shows repeated subtraction for the given number 208. 

Since the difference does not become zero, 208 is not a perfect square number and hence it does not have a perfect square root. The root lies between the numbers 14 and 15, resulting in a decimal root. 

Video Lessons

Visualising square roots

Finding Square roots

Related Articles

• Square Root
• Finding Square roots
• 1 to 50 Square and Square root List.
• Finding Square root with Example
• Square root Calculator
• Squares and Square roots.

Solved Examples

1. Which number is that lesser than or greater than 208 that has a perfect square root?

196, which is less than 208 and 225, which is greater than 208, are the perfect square numbers. 14 and 15 are their perfect square roots, respectively.

2. What is the square root of 225?

15 is the square root of 225.