Square Root of 225

The square root of 225 is equal to 15. In mathematics, the square root of any number is a value that gives the original number on multiplication by itself. If x is the square root of y, it is written as x = √y, or we can express the same equation as x² = y. Here,’√’ is the radical symbol used to denote the root of numbers. The positive number, when multiplied by itself, represents the square of the number. Also, the square root of the square of a positive number gives the original number. In this article, you will learn how to calculate the square root of 225 in different methods in detail.

What is the Square Root of 225?

The square root value of 225 is 15, i.e. √225 = 15. Here, √225 is the radical representation of the square root of 225. We know that the square of 15 is 225, i.e. 15² = 15 × 15 = 225. Thus, the square root of 225 can also be described as, √225 = √(15)² = √(15 × 15) = 15. However, the square root of 225 is ±15. This is because 15 × 15 = 225 and (-15) × (-15) = 225. From this representation, we can say that the square root of 225 can be both positive and negative of 15. In general, “the square root” is often used to refer to the principal or non-negative square root. Hence, we write the positive number as a result, unless specified as roots. Also, note that 225 is a perfect square number.

Square Root of 225 is Rational or Irrational

The square root of 225 is rational since the value of square root 225 is 15, is a whole number and it can be expressed in the form of p/q, where q is not equal to 0.

How to Find the Square Root of 225?

Square Root of 225 by the Repeated Subtraction Method

Let’s learn how to find the square root of 225 by the repeated subtraction method.

• 225 – 1 = 224
• 224 – 3 = 221
• 221 – 5 = 216
• 216 – 7 = 209
• 209 – 9 = 200
• 200 – 11 = 189
• 189 – 13 = 176
• 176 – 15 = 161
• 161 – 17 = 144
• 144 – 19 = 125
• 125 – 21 = 104
• 104 – 23 = 81
• 81 – 25 = 56
• 56 – 27 = 29
• 29 – 29 = 0

Thus, starting from 225, we have subtracted 15 times to obtain 0. Therefore, the square root of 225 is 15.

Learn about the square root of a number by the repeated subtraction method here.

Square Root of 225 by Prime Factorization

First, write the prime factors of 225.

Prime factorization of 225 = 3 x 3 x 5 x 5

i.e. 225 = 3 x 3 x 5 x 5

Now, represent these prime factors in pairs.

225 = (3 x 3) x (5 x 5)

Take square root on both sides.

√225 = √(3 x 3) x (5 x 5) = 3 x 5 = 15

Therefore, √225 = 15.

Square Root of 225 by Division Method

Go through the steps given below, to learn how to find the square root of 225 by the long division method.

Step 1: Write 225 and take the digits of the number in pairs from the right. So, from 225, 25 is chosen as a pair, and 2 stands alone.

Step 2: We need to divide 1 with a number such that the number × number gives 1 or a number less than that.

Step 3: Now, we got 1 as the quotient and 1 as the remainder.

Step 4: Let’s bring down 25 for division so that the new dividend becomes 125.

Step 5: Double the divisor, that means 1 + 1 = 2. Write this as one of the digits for the new divisor.

Step 6: Identify a number that can be placed next to 2 to obtain a two-digit number as a new divisor. Also, the number set here should be multiplied by itself to produce 125 or less than that.

Step 7: We find that 5 is the number, such that 25 × 5 gives 125.

Step 8: Now we got the quotient 15, and the remainder as 0.

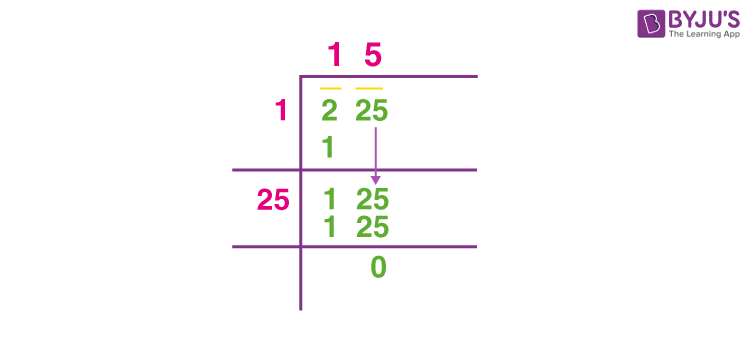
Hence, the square root of 225 is 15.

Get the square roots of more numbers here.

Square root of 64 = 8

Square root of 169 = 13

Square root of 256 = 16

Square root of 400 = 20

Square root of 100 = 10

Square root of 144 = 12

Video Lessons on Square Roots

Visualising square roots

Finding Square roots

Solved Example

Question

If the area of a square-shaped field is 225 m², the length of each side of the field.

Solution:

Given,

Area of the square field = 225 m²

As we know, the area of a square of the side “a” = a²

So, a² = 225

a = 225 = 15 {a cannot be -15 since the side measure cannot be negative}

Therefore, the side of the square field is 15 m.