Square Root of 529

Square root of 529 is 23 and is represented as √529 = 23. 

Consider the numbers 25, 36, 49… These are obtained by multiplying a number with itself. i,e 25 = 5 × 5, 36 = 6 × 6 and 49 = 7 × 7 and so on. The numbers 25, 36, 49 are termed as perfect square numbers and 5, 6, 7 are termed as square roots for 25, 36 and 49 respectively. If the number 529 is a perfect square, then there will be an integer “y” such that “y ×y” = 529, where “y” will be the square root of 529. Let us determine the value of “y” using different methods that are detailed below.

Note the Following:

The Square root of 529 = √529 where √ = radical, and 529 is the radicand.

Exponential Form of Square root of 529 = 529^1/2. 

Solution for √529 = 23

Square root of 529 is Irrational = Fasle

For the detailed explanation on square roots can be obtained from Squares and Square roots.

What is the Square root of 529?

The square root of 529 is 23. In other words, the square of 23 is 529. i.e ±23 × ±23 is 529. 

How to Find the Square root of 529?

There are three methods to find the Square root of 529:

• Prime Factorisation method
• Long Division method
• Repeated Subtraction method

Square root of 529 by Prime Factorisation Method

In the Prime Factorisation method, the following steps are followed;

1. Divide 529 by prime divisors. Only 23 divided 529.
2. Since 23 x 23 is 529, 23 is the square root. 

Division for 529 is;

529 = 23 × 23 

529 = (23 × 23)

√529 = √(23 × 23)

√529 = 23

Therefore the square root of 529 = 23.

Square root of 529 by Long Division Method

In the long division method, the given numbers are paired in groups, starting from the right side. Let us understand the long division method, in detailed steps;

Step 1:  Grouping the given number into pairs

Given number is 529, grouping it as 2 and 56.

Step 2: Consider the first number.

Let us find a square number that divides the first number

i.e 1 × 1 = 1 

2 × 2 = 4 

3 × 3 = 9.

Step 3: Continue the division using the next number 29. The first number to be used as the next divisor (Divisor of first division multiplied by quotient of first division)

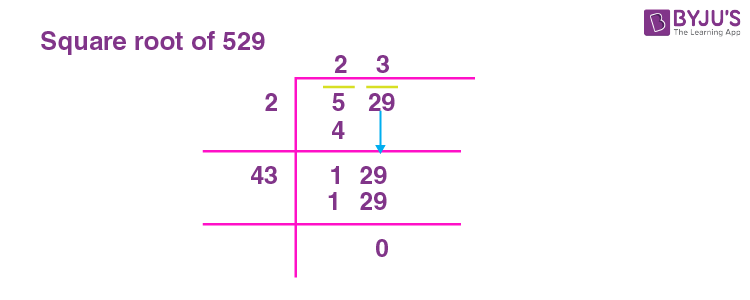
The Division completes with zero remainder. Hence the quotient is the square root, which is 23 for 529. 

Square root of 529 by Repeated Subtraction Method.

In the repeated subtraction method, the number 529 is decreased repeatedly by odd numbers. This results in

1. Difference = zero; Then 529 is a perfect square with the perfect square root.
2. Difference = negative; Then 529 is not a perfect square and it has an irrational root. 

For the given number 529, steps for repeated subtraction are

Step 23 leads to the difference zero, which implies that 529 is a perfect square number and hence 23 is its root. 

Video Lessons

Visualising square roots

Finding Square roots

Related Articles

• Square Root.
• What is Square root?
• Finding Square roots
• 1 to 50 Square and Square root List
• Finding Square root with Example
• Square root Calculator

Solved Examples

1. Find the square root of 529 by pairing factors.

The pairs of 529 are (1, 529) and (23, 23)

Therefore the square root of 529 is 23 using pairing factors 23 and 23. 

2. What is the square of 23?

The square of 23 is nothing but 23 times 23 and that is 529.