Standard Identities

Standard Identities

Consider the following equation:

2(x+3) = 2x+6

What can you say about the above equation? In LHS, if you substitute the value of x =3, you will get 12. Even in RHS, if you substitute the value of the variable x with 3, you will get 12 as the answer.

In mathematics, an equation P = Q is called an identity if the following conditions are satisfied:

1. Both sides of the equality relation contain some variables.
2. Both the sides give the same value when the variable is substituted with a particular constant.

If an equality relation satisfies the above two conditions, it will be an identity. There can be many relations in mathematics that can be called identities, but we need not need to remember all of them. Few standard identities of maths are important in algebra, which can make the calculations simple.

Also, learn: Algebra

List of Standard Identities

The standard identities (algebraic), i.e., the standard identities of algebra are as follows:

• (a + b)² = a² + b² + 2ab
• (a – b)² = a² + b² – 2ab
• (a + b)³ = a³ + b³ + 3ab(a + b) = a³ + b³ + 3a²b + 3ab²
• (a – b)³ = a³ – b³ – 3ab(a – b) = a³ – b³ – 3a²b + 3ab²
• (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
• a³ – b³ = (a – b)(a² + ab + b²)
• a³ + b³ = (a + b)(a² – ab + b²)
• a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – ab – bc – ca)

Standard Identities with Proof 

Let us try to prove the first identity and see whether it is valid or not.

Consider the LHS,

(a + b)² = (a + b) x (a + b)

= a(a + b) + b(a + b)

= a² + ab + ab + b²

= a² + b² + 2ab

Let us try to prove the above equality relation in another way.

Consider a square of a side (a + b) divided into the following rectangles and squares:

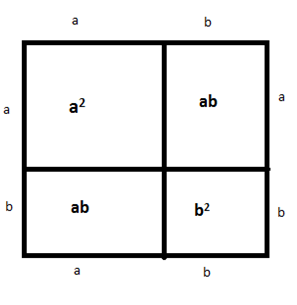
The total area is given as the sum of areas of each figure, i.e. a² + ab + ab + b²  = a² + b² + 2ab, which is equal to RHS. Hence the identity is valid. Therefore, whatever is the method of proving the identity it will always be true.

The standard identities discussed above are the algebraic identities. These standard identities hold true for any value of the variable.

Standard identities of Trigonometry

There exist some standard identities in trigonometry that involve all the six trigonometric ratios. They are:

• sin²θ + cos²θ = 1
• sec²θ – tan²θ = 1
• cosec²θ – cot²θ = 1

Get more trigonometric identities here.

Standard Identities of Algebraic Expressions Examples

Example 1: 

Use a suitable identity to simplify (x – 4)(x – 4).

Solution:

(x – 4)(x – 4) = (x – 4)²

Using the identity (a – b)² = a² – 2ab + b²,

(x – 4)² = x² – 2(x)(4) + (4)²

= x² – 8x + 16

Example 2: 

Solve (2p – 3q)(2p + 3q) using a suitable identity.

Solution:

(2p – 3q)(2p + 3q)

Using the identity (a – b)(a + b) = a² – b²

So, 

(2p – 3q)(2p + 3q) = (2p)² – (3q)²

= 4p² – 9q²

To learn more about algebra related topics, download BYJU’S – The Learning App today!