The best possible way to understand Mathematics subject is to refer to the MP Board Class 9 Maths Syllabus that gives an oview of the topics and concepts covered in Class. Mathematics may be a nightmare for many, but learning Mathematics the right way will make it one of the simplest and most favourite subjects. To achieve this, Mathematics should be practised in coherence with the MP Board 9th Class Maths Syllabus. MPBSE has a group of experts who designed the syllabus in the simplest possible way.
Class 9 syllabus 2021-2022 under Madhya Pradesh board gives a brief introduction to Mathematical modelling and different proofs in mathematics, covering the major topics like Number Systems, Algebra, Coordinate Geometry, Geometry, Mensuration, Statistics and Probability. The final exam for class 9 MP board will be conducted for 100 marks and lasts for 3 hours. Total preparation time will be 180 hours. Thus, 180 hours of serious preparation will be sufficient to outshine in the final examination.
MP Board Class 9 Maths Syllabus 2021-2022 PDF
Find here the chapter details in Hindi, from the latest reduced syllabus for Maths.
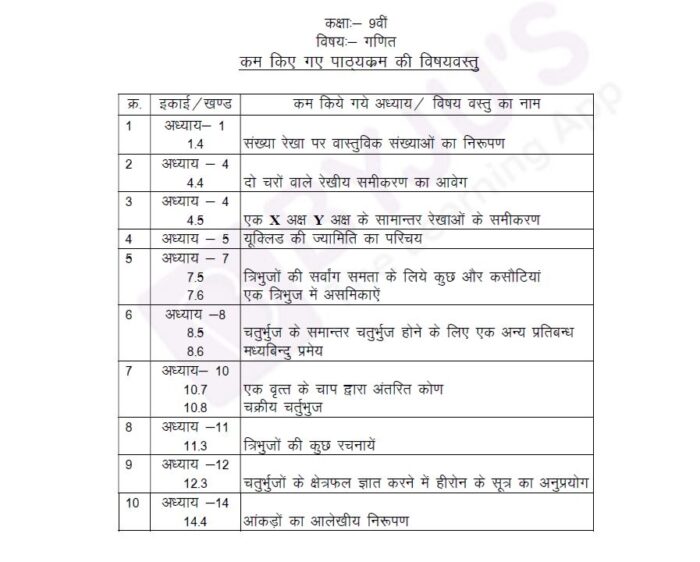
Meanwhile, check the below table for a detailed description of the previous 2020-21 syllabus for class 9th MP board.
Class 9th Maths Syllabus for MP Board 2021-22 |
|
| Unit 1 | Number Systems
Real Numbers Review of representation of natural numbers, integers, rational numbers on the number line. Representation of terminating/non-terminating recurring decimals, on the number line through successive magnification. Rational numbers as recurring/terminating decimals. Examples of non recurring non terminating decimals such as etc. Existence of non-rational numbers (irrational numbers: such as and their representation on the number line. Explaining that every real number is represented by a unique point on the number line, and conversely, every point on the number line represents a unique real number. Existence of for a given positive real number x (visual proof to be emphasized). Definition of nth root of a Real number. Recall of laws of exponents with integral powers. Rational exponents with positive real bases (to be done by particular cases, allowing the learner to arrive at the general laws). Rationalisation (with precise meaning) of real numbers of the type (and their combinations). , where X and Y are natural numbers and a. b are integers |
| Unit 2 | Algebra
Definition of a polynomial in one variable, its coefficients, with examples and counter examples, Its terms, zero polynomial Degree of a polynomial. Constant, linear, quadratic, cubic polynomials; monomials, binomials. Trinomials. Factors and multiples. Zeros/roots of a polynomial/equation. State and motivate the Remainder Theorem with examples and analogy to integers. Statement and proof of the Factor Theorem. Factorisation of where a,b,c are real numbers and of cubic polynomials using the Factor Theorem. Recall of algebraic expressions and identities. Further identities of the type: Linear Equations in Two Variables Recall of linear equations in one variable. Introduction to the aqua don in ban variables Prove that a linear equation in two variables has infinitely many solutions, and justify their being written as ordered pairs of real numbers. plotting them and showing that they seem to lie on a line. Examples, problems from real life, including problems on Ratio and Proportion and with algebraic and graphical solutions being done simultaneously. |
| Unit 3 | Coordinate Geometry
The Cartesian plane, coordinates of a point, names and terms associated with the coordinate plane, notations, plotting points in the plane, graph of linear equations as examples; focus on linear equations of the type ax+by+c=0 by writing it as y=mx+c and linking with the chapter on linear equations in two variables. |
| Unit 4 | Geometry
Introduction to Euclid’s Geometry History. – Euclid and geometry in India Euclid’s method of formalizing observed phenomenon into rigorous mathematics with definitions, common/obvious notion, axioms postulates, and theorems. The5 postulates of Euclid’s Equivalent versions of the fifth postulate. Showing the relationship between axiom and theorem. I. Given two distinct points. there exists one and only one line through them. 2. (Prove) Two distinct lines cannot have more than one point in common. Lines and Angles I. (Motkatt; if a ray stands on a line then the sum of the two adjacent angles so formed is 180° and the converse. 2. (Prove) If two lines intersect, vertically opposite angles are equal. 3. (Motivate) Results on corresponding angles, alternate angles, interior angles when a transversal intersects two parallel liner. 4. (Motivate) lines, which are parallel to a given line. are parallel. 3. (Prove) The sum of the angles of a triangle is 180°. 6. (Motivate) If a side of a triangle is produced. the exterior angle so formed is equal to the sum of the two interior opposite angles. Triangles 1. (Motivate) Two triangles are congruent if any two sides and the included angle of one triangle is equal to any two sides and the included angle of the other triangle (SAS Congruence). 2. (Prove) Two triangles are congruent if any two angles and the included side of one triangle is equal to any two angles and the included side,of the other triangle (ASA Congruence). 3. (Motivate) Two triangles are congruent if the three sides of one triangle are equal to three sides of the other triangle (SSS Congruence). 4. (Motivate? Two right triangles are congruent if the hypotenuse and a side of one triangle are equal ;respectively; to the hypotenuse and a side of the other triangle. 5. (Prover The angles opposite to equal sides of a triangle are equal. 6. (Motivate) The sides opposite to equal angles of a triangle are equal. 7. (Motivate) Triangle inequalities and relations between ‘angle and facing side’; inequalities in a triangle Quadrilaterals 1. (Prove; The diagonal divides a parallelogram into two congruent triangles. 2. (Motivate; in a triangle opposite side are equal and conversely 3. (Motivate) In a parallelogram opposite angles are equal and conversely. 4. (Motivate) A quadrilateral is a parallelogram if a pair of its opposite sides are parallel and equal. 5. (Motivate) In a parallelogram, the diagonals bisect each other and conversely. 6. (Motivate) In a triangle, the line segment joining the mid points of any two sides is parallel to the third side and (motivate) its converse. Area Review concept of area, recall arca of a rectangle.
1. (Prove) Parallelograms on the same base and between the same parallels have the same area. 2. (Motivate) Triangles on the same base and between the same parallels are equal in area and its converse. Circles Through examples, arrive at definitions of circle related concepts, radius, circumference, diameter, chord, arc, subtended angle. 1. (Prove) Equal chords Cif a circle subtend equal angles at the centre and (motivate) its converse. 2. (Motivate) The perpendicular from the centre of a circle to a chord bisects the chord and conversely, the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord. 3. (Motivate) There is one and only one circle passing through the given non-collinear points. 4. (Motivate) Equal chords of a circle (or of congruent circles) are equidistant from the centre(s) and conversely 5. (Prove) The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle. 6. (Motivate) Angles in the same segment of a circle are equal. 7. (Motivate) If a line segment joining two points subtends equal angle at two other points lying on the same side of the line containing the segment, the four points lie on a circle. 8. (Motivate) The sum of either pair of opposite angles of a cyclic quadrilateral is 180 degrees and its converse. Constructions 1. Construction of bisectors of a line segment and angle, 69°, 911°, 45° angles etc, equilateral triangles. 2. Construction of a triangle given its base, sum/difference of the other two sides and one base angle. 3. Construction of a triangle of given perimeter and base angles. |
| Unit 5 | Mensuration
Areas Area of a triangle using Heron’s formula (without proof) and its application in finding the area of a quadrilateral. Surface Areas and Volumes Surface areas and volumes of cubes, cuboids, spheres (including hemispheres) and right circular cylinders/cones |
| Unit 6 | Statistics and Probability
Statistics Introduction to Statistics: Collection of data, presentation of data — tabular form, ungrouped/ grouped, bar graphs, histograms (with varying base lengths), frequency polygons, qualitative analysis: of data to choose the correct form of presentation for the collected data. Mean, median, mode of ungrouped data. Probability History, Repeated experiments and observed frequency approach to probability. Focus is on empirical probability. (A large amount of time to be devoted to group and to individual activities to motivate the concept; the experiments to be drawn from real-life situations. and from examples used in the chapter on statistics). |
| Appendix | 1. Proofs in Mathematics
What a statement. is; when-is a statement mathematically valid. explanation Of axiom/ postulate through familiar examples Difference between axiom, conjecture and theorem. The concept and nature of a ‘proof’ (emphasize deductive nature of the proof. The assumptions, the hypothesis, the logical argument) and writing a proof. Illustrate deductive proof with complete arguments using simple results from arithmetic. Algebra and geometry (cg, product of two odd numbers is odd etc.). Particular stress on verification not being proof. Illustrate with a few examples of verifications leading to wrong conclusions — include statements like “every odd number greater than I is a prime number”. What disproving means, use of counter examples. 2. Introduction to Mathematical Modelling The concept of mathematical modelling, review of work done in earlier classes while looking at situational problems. aims of mathematical modelling. discussing the broad stages of modelling — real-life shua thins, setting up of hypothesis, determining an appropriate model, solving the mathematical problem equivalent, analyzing the conclusions and their real-life interpretation, validating the model. Examples to be drawn from ratio, proportion, percentages, etc. |
Students can also access other study material and resources of MP Board Class 9 from BYJU’S.
Find also resources for mp board 10th class here.

Comments