MSBSHSE Solutions For Class 8 Maths Part 2 Chapter 17 Circle - Chord and Arc

MSBSHSE Solutions For Class 8 Maths Part 2 Chapter 17 Circle – Chord and Arc are provided here for students to assist in their preparations and score high marks in their examinations. Practise is much needed to achieve good marks in Mathematics as it’s a scoring subject. Here, in this chapter students will learn about the properties of chord of a circle, arcs corresponding to chord of a circle and congruent arcs. All the solutions are formulated by individual subject experts, in order to help students understand the concepts and methods to solve problems quickly. MSBSHSE Solutions for Class 8 are of immense help to students aiming to secure high marks in the examinations. All the solutions are created keeping in mind the latest Maharashtra board guidelines for effective preparations. The solutions to the Maharashtra Board Solutions for Class 8 Maths Chapter 17 Circle – Chord and Arc can be easily downloaded by the students, from the link mentioned below.

Download the PDF of Maharashtra Board Solutions For Class 8 Maths Part 2 Chapter 17 Circle – Chord and Arc

Access answers to Maharashtra Board Solutions For Class 8 Maths Part 2 Chapter 17 Circle – Chord and Arc.

Practice Set 17.1 Page No: 116

1. In a circle with centre P, chord AB is drawn of length 13 cm, seg PQ ⊥ chord AB, then find l(QB).

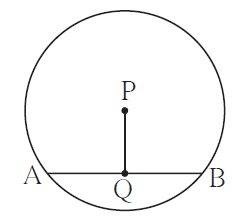
Solution:

Given,

seg PQ ⊥ chord AB and l(AB) = 13 cm

Now,

l(QB) = ½ l(AB

⇒ l(QB) = ½ x 13

Thus, l(QB) = 6.5 cm

2. Radius of a circle with centre O is 25 cm. Find the distance of a chord from the centre if length of the chord is 48 cm.

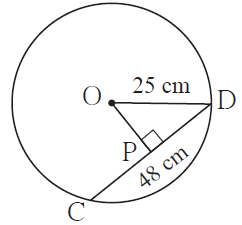
Solution:

Given,

seg OP ⊥ chord CD and l(CD) = 48 cm

Radius of circle = 25 cm, so OD = 25 cm

Now,

l(PD) = ½ l(CD)

l(PD) = ½ x 48

⇒ l(PD) = 24 cm … (i)

In ∆OPD, we have

m ∠OPD = 90°

So, by Pythagoras theorem

(25)² = [l(OP)]² + (24)² [From (i)]

(25)² – (24)² = [l(OP)]²

(25 + 24) (25 – 24) = [l(OP)]² [Since, a² – b² = (a + b) (a – b)]

49 x 1 = [l(OP)]²

∴l(OP) = √49 = 7 cm [Taking square root of both sides]

Thus, the distance of the chord from the centre of the circle is 7 cm.

3. O is centre of the circle. Find the length of radius, if the chord of length 24 cm is at a distance of 9 cm from the centre of the circle.

Solution:

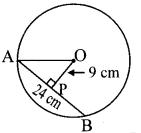Let seg OP ⊥ chord AB

l(AB) = 24 cm and l(OP) = 9 cm

Now,

l(AP) = ½ l(AB)

l(AP) = ½ x 24

⇒ l(AP) = 12 cm …(i)

In ∆OPA, we have

m ∠OPA = 90°

So, by Pythagoras theorem

= 81 + 144 = 225

⇒ l(AO) = √225 = 15 cm [Taking square root of both sides]

Thus, the length of radius of the circle is 15 cm.

4. C is the centre of the circle whose radius is 10 cm. Find the distance of the chord from the centre if the length of the chord is 12 cm.

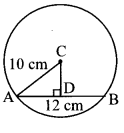Solution:

Let’s consider a circle of radius 10 cm and centre C.

And, seg AB be the chord of the circle

Now, draw seg CD ⊥ chord AB, l(AB) = 12 cm and l(AC) = 10 cm.

l(AD) = ½ l(AB)

l(AD) = ½ x 12

⇒ l(AD) = 6 cm …(i)

So,

In ∆ACD, m ∠ADC = 90°

By Pythagoras theorem,

(10)² = (6)² + [l(CD)]² [From (i) and l(AC) = 10 cm]

(10)² – (6)² = [l(CD)]²

100 – 36 = [l(CD)]²

64 = [l(CD)]²

⇒ l(CD) = √64 = 8 cm [Taking square root of both sides]

Thus, the distance of the chord from the centre of the circle is 8 cm.

Practice Set 17.2 Page No: 118

1. The diameters PQ and RS of the circle with centre C are perpendicular to each other at C. State, why arc PS and arc SQ are congruent. Write the other arcs which are congruent to arc PS.

Solution:

Given, diameter PQ ⊥ diameter RS

So, we have

m ∠PCS = m ∠SCQ = m ∠PCR = m ∠RCQ = 90°

We know that, the measure of the angle subtended at the centre by an arc is the measure of the arc.

So,

m (arc PS) = m ∠PCS = 90° … (i)

m (arc SQ) = m ∠SCQ = 90° … (ii)

From (i) and (ii), we see that

m (arc PS) = m (arc SQ)

Hence, arc PS ≅ arc SQ

Similarly,

m (arc PR) = m ∠PCR = 90° … (iii)

m (arc RQ) = m ∠RCQ = 90° … (iv)

Hence, from (i), (iii) and (iv) we have

m (arc PS) = m (arc PR) = m (arc RQ)

∴ arc PS ≅ arc PR ≅ arc RQ

Thus, arc PR and arc RQ are congruent to arc PS.

2. In the adjoining figure O is the centre of the circle whose diameter is MN. Measures of some central angles are given in the figure. Hence find the following

(1) m ∠ AOB and m ∠ COD

(2) Show that arc AB ≅ arc CD.

(3) Show that chord AB ≅ chord CD

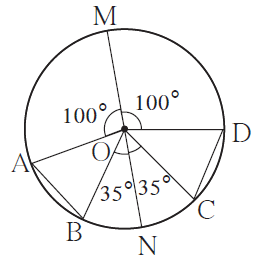
Solution:

(1) Given,

Seg MN is the diameter of the circle and m ∠AOM = 100°, m ∠BON = 35°, m ∠DOM = 100° and m ∠CON = 35°

Now,

m ∠AOM + m ∠AON = 180° [Angles in a linear pair]

m ∠AOM + (m ∠AOB + m ∠BON) = 180° [Angle addition property]

100° + m ∠AOB + 35° = 180°

m ∠AOB + 135° = 180°

m ∠AOB = 180°- 135°

⇒ m ∠AOB = 45° … (i)

Also, we have

m ∠DOM + m ∠DON = 180° [Angles in a linear pair]

m ∠DOM + (m ∠COD + m ∠CON) = 180° [Angle addition property]

100° + m ∠COD + 35°= 180°

m ∠COD + 135° = 180°

m ∠COD = 180°- 135°

⇒ m ∠COD = 45° … (ii)

(2) Now, m (arc AB) = m ∠AOB = 45° [From (i)]

And, m (arc DC) = m ∠DOC = 45° [From (ii)]

So, from (i) and (ii)

m (arc AB) = m (arc DC)

Hence,

arc AB ≅ arc CD

(3) We have, arc AB ≅ arc CD [Proved above]

Hence, as the chords corresponding to congruent arcs are congruent

chord AB ≅ chord CD.

Highly experienced subject experts at BYJU’S, having vast conceptual knowledge have developed these solutions, which match the different understanding abilities of all kinds of students. Chapter 17 discusses Circle – Chord and Arc, where students can refer to MSBSHSE Solutions to score full marks in the examination. Many such exercise problems are illustrated for students to practice and excel in their examinations.