Maharashtra SSC Maths Geometry (Paper 1) Exam Question Paper 2017 with Solutions – Free Download
MSBSHSE (Maharashtra board) Annual Exam Class 10 Maths 2017 Geometry Question Paper with solutions are provided at BYJU’S. Students can get the solutions of all the previous years’ question papers of MSBSHSE SSC Maths. These solutions are available in a downloadable pdf format for both the papers of Maths, namely Geometry and Algebra of Class 10. By practising these SSC Maths question papers, students will be able to understand the different ways of asking Maths questions in the annual examination. Students can also refer to the important questions of class 10 Maths and formulas, as a part of their preparation.
Download MSBSHSE 2017 Geometry Question Paper Maths
Download MSBSHSE 2017 Geometry Question Paper With Solutions
MSBSHSE Class 10 Mathematics Question Paper 2017 Geometry Paper with Solutions
PART – A
1. Solve any five sub-questions: [5]
(i) In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and AD = 9, find A(Δ ABE)/ A(Δ BAD).
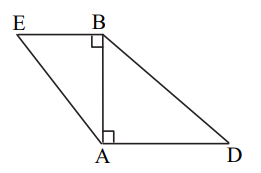
Solution:
Given,
BE = 6 and AD = 9
A(Δ ABE)/ A(Δ BAD) = [(1/2) × BE × AB]/ [(1/2) × AB × AD]
= BE/AD
= 6/9
= 2/3
(ii) If two circles with radii 8 cm and 3 cm, respectively touch internally, then find the distance between their centres.
Solution:
Given,
Two circles with radii 8 cm and 3 cm respectively touch internally.
Distance between their centres = Difference of the radii
= 8 – 3
= 5 cm
(iii) Find the height of an equilateral triangle whose side is 6 units.
Solution:
Given,
Side of an equilateral triangle = 6 units
Height (Altitude) of an equilateral triangle = (√3/2) × side
= (√3/2) × 6
= 3√3 units
(iv) If the angle θ = -45°, find the value of tan θ.
Solution:
Given,
θ = -45°
We know that,
tan (-θ) = -tan θ
Now,
tan θ = tan (-45°)
= -tan 45°
= -1
(v) Find the slope and y-intercept of the line y = 3x – 5.
Solution:
Given,
y = 3x – 5
Comparing with the equation of line having slope m and y-intercept c: y = mx + c
m = 3, c = -5
Therefore, slope = 3 and y-intercept = -5
(vi) Find the circumference of a circle whose radius is 7 cm.
Solution:
Given,
Radius of the circle = r = 7 cm
Circumference of the circle = 2πr
= 2 × (22/7) × 7
= 44 cm
2. Solve any four sub-questions: [8]
(i) In ΔPQR, seg RS is the bisector of ∠PRQ, PS = 6, SQ = 8, PR = 15. Find QR.
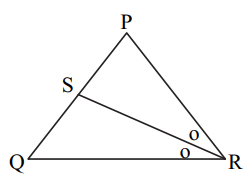
Solution:
Given,
PS = 6, SQ = 8, PR = 15
seg RS is the bisector of ∠PRQ.
By the angle bisector property,
PR/QR = PS/SQ
15/QR = 6/8
⇒ QR = (15 × 8)/6
⇒ QR = 20
(ii) In the given figure PA = 6, PB = 4 and PC = 8. Find PD.
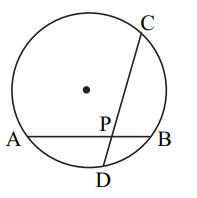
Solution:
We know that when the two chords of a circle intersect each other inside it then the product of their segments is equal.
Given,
PA = 6, PB = 4 and PC = 8
AB and CD intersect each other at P.
PA × PB = PC × PD
6 × 4 = 8 × PD
PD = (6 × 4)/8
PD = 3
(iii) Draw ∠ABC of measure 105° and bisect it.
Solution:
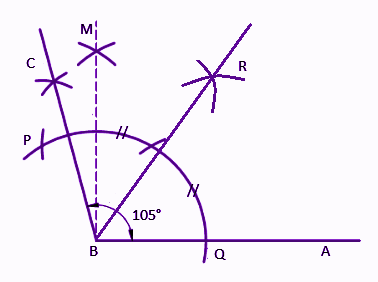
Therefore, ∠ABC = 105° and BR is its bisector.
(iv) Find the sine ratio of θ in a standard position whose terminal arm passes through (4, 3).
Solution:
Given,
Terminal arm passes through the point (3, 4)
i.e. (3, 4) = (x, y)
r = √(x2 + y2)
= √(32 + 42)
= √(9 + 16)
= √25
= 5
We know that,
y = r sin θ
sin θ = y/r = 4/5
(v) Find the slope of the line passing through the points A(6, -2) and B(-3, 4).
Solution:
Let the given points be:
A(6, -2) = (x1, y1)
B(-3, 4) = (x2, y2)
Slope of the line passing through the points (x1, y1) and (x2, y2)
= (y2 – y1)/ (x2 – x1)
= (4 + 2)/ (-3 – 6)
= 6/-9
= -2/3
Therefore, the slope is -2/3.
(vi) The dimensions of a cuboid in cm are 30 × 18 × 10. Find its volume.
Solution:
Given,
Dimensions of the cuboid = 30 cm × 18 cm × 10 cm
i.e. Length = 30 cm
Breadth = 18 cm
Height = 10 cm
Volume of the cuboid = Length × Breadth × Height
= 30 × 18 × 10
= 5400 cm3
3. Solve any three sub-questions: [9]
(i) Prove that, “If the angles of a triangle are 45°- 45°- 90°, then each of the perpendicular sides is 1/√2 times the hypotenuse.”
Solution:
Given,
ABC is a right triangle in which ∠B = 90° and ∠A = ∠C = 45°.
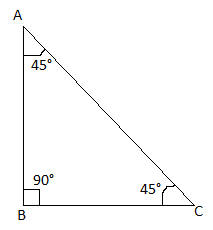
To prove: AB = BC = (1/√2) AC
Proof:
∠A = ∠C = 45°
AB = BC (sides opposite to equal angles are equal)
In right triangle ABC,
By Pythagoras theorem,
AB2 + BC2 = AC2
AB2 + AB2 = AC2
2AB2 = AC2
AB2 = (1/2) AC2
AB = (1/√2) AC
And AB = BC = (1/√2) AC
Hence proved.
(ii) Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.

Solution:
From the given,
∠APR + ∠APB = 180° (linear pair: BPR is a straight line )
110° + ∠APB = 180°
∠APB = 180° – 110°
∠APB = 70°
We know that the radius is perpendicular to the tangent through the point of contact.
∠OAP = ∠OBP = 90°
In quadrilateral OAPB,
∠APB + ∠OBP + ∠BOA + ∠OAP = 360°
70° + 90° + ∠BOA + 90° = 360°
∠BOA + 250° = 360°
∠BOA = 360° – 250°
∠BOA = 110°
Therefore, the angle between the two radii is 110°.
(iii) Construct tangents to the circle from point B, having radius 3.2 cm and centre ‘C’. Point B is at a distance of 7.2 cm from the centre.
Solution:
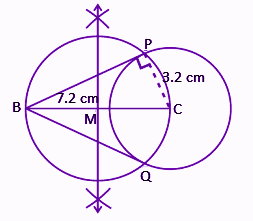
Therefore, BP and BQ are the required tangents to the circle with centre C.
(iv) From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60°. If the height of the lighthouse is 84 metres, then find how far is that ship from the lighthouse? (√3 = 1.73)
Solution:
Let AB be the lighthouse and C be the position of the ship.

AB = 84 m
In right triangle ABC,
tan 60° = AB/BC
√3 = 84/BC
BC = 84/√3
= (84/√3) (√3/√3)
= (84√3)/3
= 28√3
= 28 × 1.73
= 48.44
Hence, the distance between the ship and the lighthouse is 48.44 m.
(v) The volume of a cube is 1000 cm3. Find its total surface area.
Solution:
Given,
Volume of cube = 1000 cm3
⇒ (side)3 = (10)3
⇒ Side = 10 cm
Total surface area of cube = 6 × (side)2
= 6 × (10)2
= 6 × 100
= 600 cm2
4. Solve any two sub-questions: [8]
(i) Prove that, “The opposite angles of a cyclic quadrilateral are supplementary”.
Solution:
Given,
ABCD is a cyclic quadrilateral of a circle with centre O.
Construction: Join OB and OD.
To prove: ∠BAD + ∠BCD = 180°
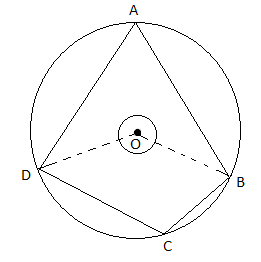
Proof:
We know that the angle subtended by the arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∠BOD = 2∠BAD….(i)
Also,
reflex∠BOD = 2∠BCD….(ii)
Adding (i) and (ii),
2∠BAD + 2∠BCD = ∠BOD + reflex ∠BOD
2(∠BAD + ∠BCD) = 360°
∠BAD + ∠BCD = 360°/2
∠BAD + ∠BCD = 180°
Hence proved.
(ii) Eliminate θ, if
x = 3 cosec θ + 4 cot θ
y = 4 cosec θ – 3 cot θ
Solution:
Given,
x = 3 cosec θ + 4 cot θ….(i)
y = 4 cosec θ – 3 cot θ….(ii)
(i) × 4 – (ii) × 3,
4x – 3y = 12 cosec θ + 16 cot θ – (12 cosec θ – 9 cot θ)
4x – 3y = 25 cot θ
cot θ = (4x – 3y)/25
Squaring on both sides,
cot2θ = [(4x – 3y)/25]2….(iii)
Now,
(i) × 3 + (ii) × 4,
3x + 4y = 9 cosec θ + 12 cot θ + 16 cosec θ – 12 cot θ
3x + 4y = 25 cosec θ
cosec θ = (3x + 4y)/25
Squaring on both sides,
cosec2θ = [(3x + 4y)/25]2….(iv)
We know that,
cosec2θ – cot2θ = 1
[(3x + 4y)/25]2 – [(4x – 3y)/25]2 = 1(1/625) [(3x + 4y)2 – (4x – 3y)2] = 1
(3x + 4y)2 – (4x – 3y)2 = 625
(iii) A toy is a combination of a cylinder, hemisphere and a cone, each with radius 10 cm as shown in the figure. Height of the conical part is 10 cm and the total height is 60 cm. Find the total surface area of the toy. (π = 3.14, √2 = 1.41)
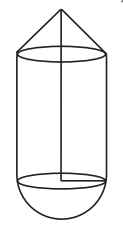
Solution:
Given,
Radius of cylinder = Radius of hemisphere = Radius of cone = r = 10 cm
Height of the conical part = h = 10 cm
Total height of the toy = 60 cm
Height of the cylinder = H = 60 – 10 – 10 = 40 cm
Slant height of cone = l = √(r2 + h2)
= √(102 + 102)
= √(100 + 100)
= √200
= 10√2 cm
Total surface area of the toy = CSA of cone + CSA of cylinder + CSA of hemisphere
= πrl + 2πrh + 2πr2
= π[10 × 10√2 + 2 × 10 × 40 + 2 × 10 × 10]
= 3.14 [100√2 + 800 + 200]
= 3.14 [100 × (1.41) + 1000]
= 3.14 [141 + 1000]
= 3.14 × 1141
= 3582.74 cm2
Hence, the total surface area of the toy is 3582. 74 cm2.
5. Solve any two sub-questions: [10]
(i) In the given figure, AD is the bisector of the exterior ∠A of ΔABC. Seg AD intersects the side BC produced in D. Prove that: BD/CD = AB/AC
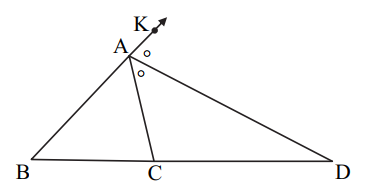
Solution:
Given,
AD is the bisector of the exterior ∠A of ΔABC.
Also, Seg AD intersects the side BC produced in D.
Draw EC || AD.
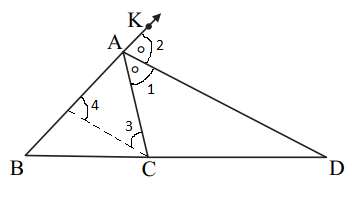
EC || AD
Thus, AC is the transversal.
∠1 = ∠3 (alternate interior angles)
∠2 = ∠4 (corresponding angles on the same side of the transversal)
∠1 = ∠2 (AD os the angle bisector of ∠A)
Also, ∠4 = ∠3
Therefore, AC = AE….(i) (sides opposite to equal angles are equal)
In triangle ABD,
EC || AD
By BPT,
BD/CD = AB/AE
BD/CD = AB/AC [From (i)]
Hence proved.
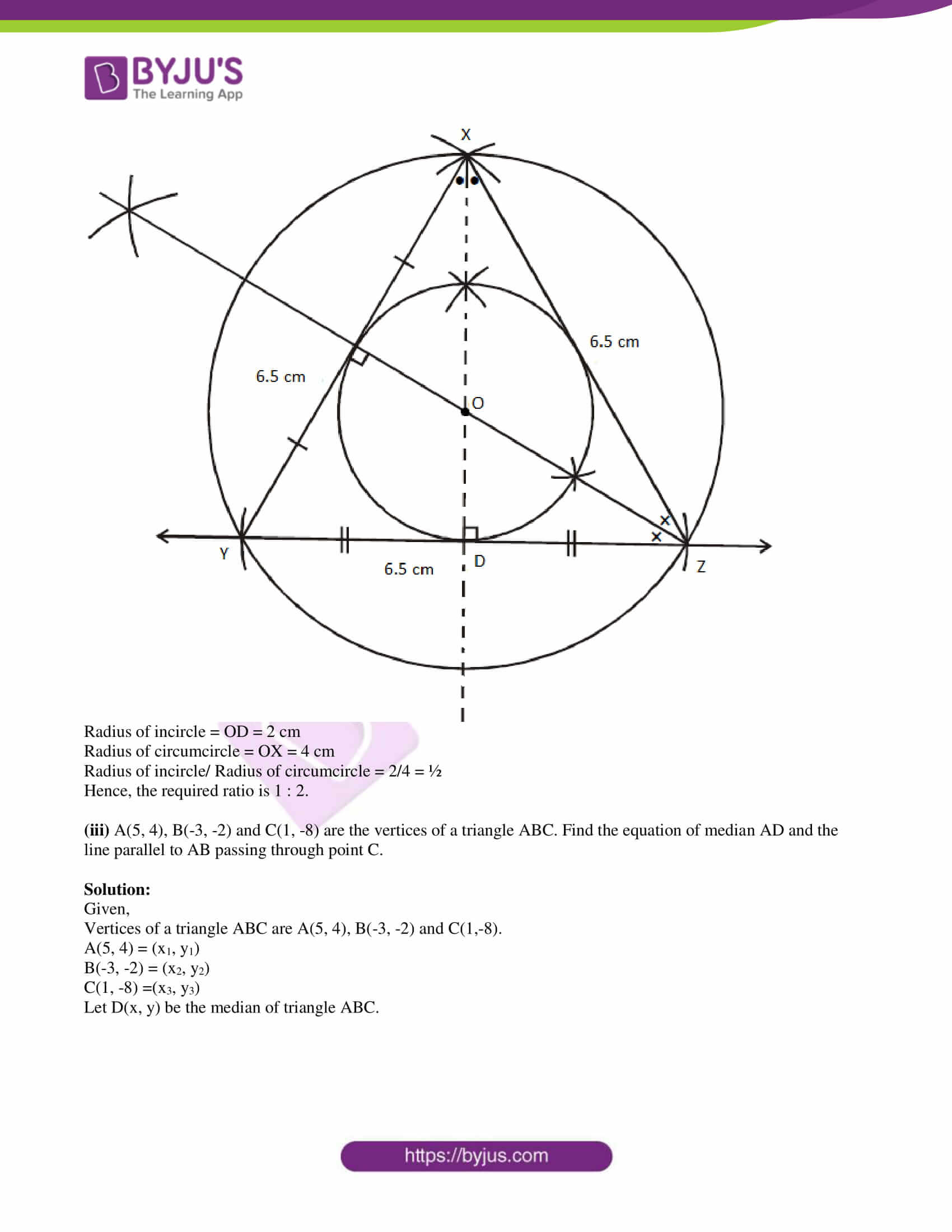
(ii) Construct the circumcircle and incircle of an equilateral ΔXYZ with side 6.5 cm and centre O. Find the ratio of the radii of incircle and circumcircle.
Solution:
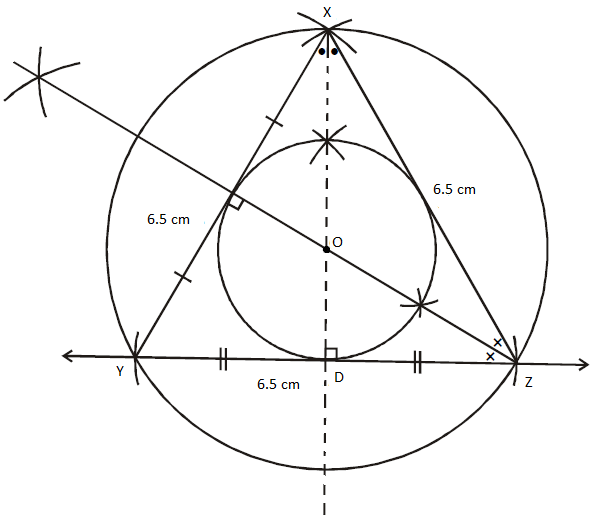
Radius of incircle = OD = 2 cm
Radius of circumcircle = OX = 4 cm
Radius of incircle/ Radius of circumcircle = 2/4 = ½
Hence, the required ratio is 1 : 2.
(iii) A(5, 4), B(-3, -2) and C(1, -8) are the vertices of a triangle ABC. Find the equation of median AD and the line parallel to AB passing through point C.
Solution:
Given,
Vertices of a triangle ABC are A(5, 4), B(-3, -2) and C(1,-8).
A(5, 4) = (x1, y1)
B(-3, -2) = (x2, y2)
C(1, -8) =(x3, y3)
Let D(x, y) be the median of triangle ABC.
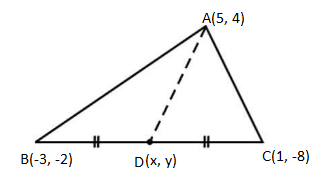
D is the midpoint of BC.
D(x, y) = [(x2 + x3)/2, (y2 + y3)/2]
= [(-3 + 1)/2, (-2 – 8)/2]
= (-2/2, -10/2)
= (-1, -5)
D(-1, -5) = (x4, y4)
Equation of median AD is
(x – x1)/ (x4 – x1) = (y – y1)/(y4 – y1)
(x – 5)/ (-1 – 5) = (y – 4)/ (-5 – 4)
(x – 5)/(-6) = (y – 4)(-9)
-9(x – 5) = -6(y – 4)
-9x + 45 = -6y + 24
9x – 45 – 6y + 24 = 0
9x – 6y – 21 = 0
3(3x – 2y – 7) = 0
3x – 2y – 7 = 0
Hence, the required equation of median AD is 3x – 2y – 7 = 0.
We know that the line parallel to AB = Slope of AB
Slope of AB = (y2 – y1)/ (x2 – x1)
= (-2 – 4)/ (-3 – 5)
= -6/-8
= 3/4
Thus, m = 3/4
Equation of the line parallel to AB and passing through the point C(1, -8) is
y – y3 = m(x – x3)
y – (-8) = (3/4)(x – 1)
4(y + 8) = 3(x – 1)
4y + 32 = 3x – 3
3x – 3 – 4y – 32 = 0
3x – 4y – 35 = 0












Please find here the link to access the previous year papers for the respective Classes. You can go to the respective class and find the year wise PDFs for the required subject.