The NCERT Exemplar Class 11 Physics Chapter 3 Motion in a Straight Line is a significant resource for students who are preparing for CBSE Class 11 examination and entrance examinations like JEE Main, JEE Advanced, NEET, and other state entrance examinations.
The NCERT Exemplar Class 11 Physics Chapter 3 PDF has questions from NCERT exemplar together with motion in a straight line extra questions, important questions from previous years’ question papers and sample papers, motion in a straight line IIT JEE problems, motion in a straight line objective questions, match the following questions, fill in the blanks, worksheets and exercise that will help you grasp the topic thoroughly. Motion in a straight line can simply be defined as the change of position of an object with respect to its surroundings in time. When motion occurs in a straight line, it can be called linear motion.
Some of the major concepts that are introduced in this chapter are listed below.
- Rest
- Motion
- Speed
- Types of Motion
- Different Graphs of Motion
The Important Topics Involved in Chapter 3 Motion in a Straight Line
- Position, path length and displacement
- Average velocity and average speed
- Instantaneous velocity and speed
- Acceleration
- Kinematic equations for uniformly accelerated motion
- Relative velocity
Download the PDF of the NCERT Exemplar Class 11 Physics Chapter 3 Motion in a Straight Line
Access Solutions for the NCERT Exemplar Class 11 Chapter 3
Multiple Choice Questions I
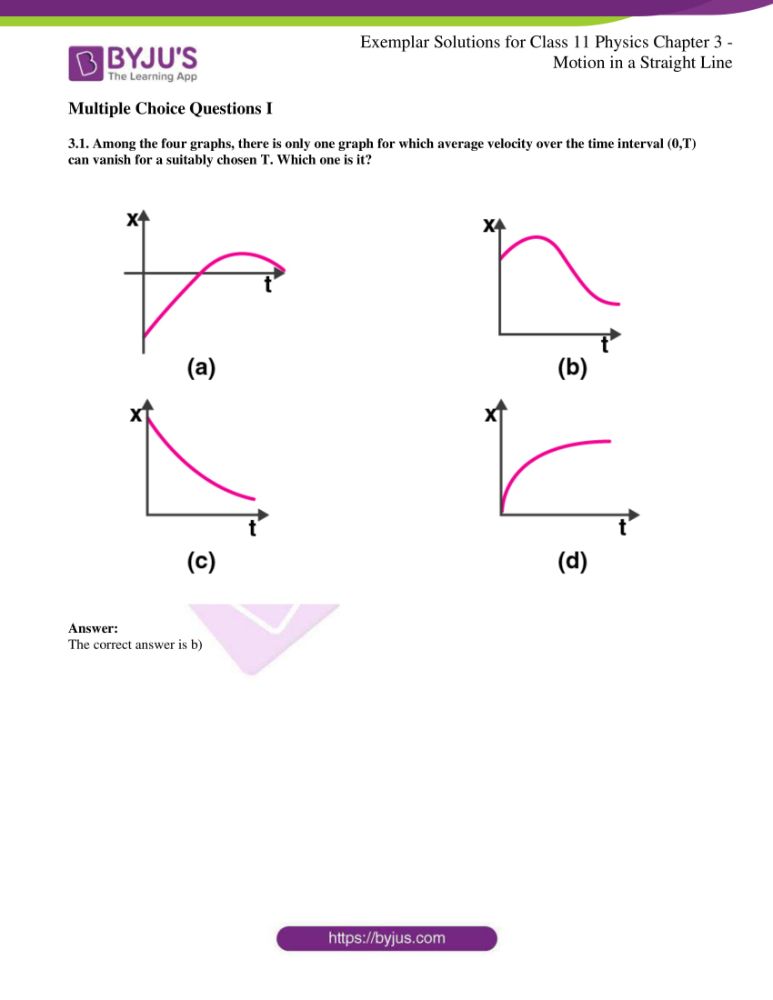
3.1. Among the four graphs, there is only one graph for which average velocity over the time interval (0,T) can vanish for a suitably chosen T. Which one is it?

Answer:
The correct answer is b)

3.2. A lift is coming from 8th floor and is just about to reach 4th floor. Taking ground floor as origin and positive direction upwards for all quantities, which one of the following is correct?
a) x<0, v<0, a>0
b) x>0, v<0, a<0
c) x>0, v<0, a>0
d) x>0, v>0, a<0
Answer:
The correct answer is a) x<0, v<0, a<0
The value of x and v becomes negative as the lift is moving from 8th floor to the 4th floor whereas acceleration is acting in the upwards and stays positive. This is explained with the help of following diagram:

3.3. In one-dimensional motion, instantaneous speed v satisfies 0≤v<v0.
a) the displacement in time T must always take non-negative values
b) the displacement x in time T satisfies: v0T<x<v0T
c) the acceleration is always a non-negative number
d) the motion has no turning points
Answer:
The correct answer is b) the displacement in time T must always take non-negative values
3.4. A vehicle travels half the distance L with speed V1 and the other half with speed V2, then its average speed is
a) (V1+V2)/2
b) (2V1+V2)/(V1+V2)
c) (2V1V2)/(V1+V2)
d) L(V1+V2)/V1V2
Answer:
The correct answer is c) (2V1V2)/(V1+V2)
3.5. The displacement of a particle is given by x = (t-2)2 where x is in metres and t is seconds. The distance covered by the particle in first 4 seconds is
a) 4 m
b) 8 m
c) 12 m
d) 16 m
Answer:
The correct answer is b) 8 m
3.6. At a metro station, a girl walks up a stationary escalator in time t1. If she remains stationary on the escalator, then the escalator take her up in time t2. The time taken by her to walk up on the moving escalator will be
a) (t1 + t2)/2
b) t1t2/(t2 – t1)
c) t1t2/(t2 + t1)
d) t1 – t2
Answer:
The correct answer is c) t1t2/(t2 + t1)
Multiple Choice Questions II
3.7. The variation of quantity A with quantity B, plotted in figure describes the motion of a particle in a straight line.

a) quantity B may represent time
b) quantity A is velocity if motion is uniform
c) quantity A is displacement if motion is uniform
d) quantity A is velocity if motion is uniformly accelerated
Answer:
The correct answer is a) quantity B may represent time, c) quantity A is displacement if motion is uniform and d) quantity A is velocity if motion is uniformly accelerated
3.8. A graph of x versus t is shown in the figure. Choose correct alternatives from below.

a) the particle was released from rest at t=0
b) at B, the acceleration a>0
c) at C, the velocity and the acceleration vanish
d) average velocity for the motion A and D is positive
e) the speed at D exceeds that at E
Answer:
The correct answer is a) the particle was released from rest at t=0, c) at C, the velocity and the acceleration vanish and e) the speed at D exceeds that at E
3.9. For the one-dimensional motion, describe by x = t – sint
a) x(t)>0 for all t>0
b) v(t)>0 for all t>0
c) a(t)>0 for all t>0
d) v(t) lies between 0 and 2
Answer:
The correct answer is a) x(t)>0 for all t>0 and d) v(t) lies between 0 and 2
3.10. A spring with one end attached to a mass and the other to a rigid support is stretched and released.
a) magnitude of acceleration, when just released is maximum
b) magnitude of acceleration, when at equilibrium position is maximum
c) speed is maximum when mass is at equilibrium position
d) magnitude of displacement is always maximum whenever speed is minimum
Answer:
The correct answer is a) magnitude of acceleration, when just released is maximum and c) speed is maximum when mass is at equilibrium position
3.11. A ball is bouncing elastically with a speed 1 m/s between walls of a railway compartment of size 10 m in a direction perpendicular to walls. The train is moving at a constant velocity of 10 m/s parallel to the direction of motion of the ball. As seen from the ground,
a) the direction of motion of the ball changes every 10 seconds
b) speed of ball changes every 10 seconds
c) average speed of ball over any 20 seconds intervals is fixed
d) the acceleration of ball is the same as from the train
Answer:
The correct option is b) speed of ball changes every 10 seconds, c) average speed of ball over any 20 seconds intervals is fixed and d) the acceleration of ball is the same as from the train
Very Short Answers
3.12. Refer to the graphs below and match the following:

| Graph | Characteristics |
| a) | i) has v > 0 and a < 0 throughout |
| b) | ii) has x > 0 throughout and has a point with v = 0 and a point with a = 0 |
| c) | iii) has a point with zero displacement for t > 0 |
| d) | iv) has v < 0 and a > 0 |
Answer:
a) matches with iii) has a point with zero displacement for t > 0
b) matches with ii) has x>0 throughout and has a point with v = 0 and a point with a = 0
c) matches with iv) has v < 0 and a > 0
d) matches with i) has v > 0 and a < 0 throughout
3.13. A uniformly moving cricket ball is turned back by hitting it with a bat for a very short time interval. Show the variation of its acceleration with taking acceleration in the backward direction as positive.
Answer:
The force which is generated by the bat is known as impulsive force. When the effect of gravity is ignored, it can be said that the ball moves with a uniform speed horizontally and returns back to the bat with the same speed. When the ball hits the bat, the acceleration is zero. Acceleration is generated when the ball strikes the bat and an impulsive force is generated.

Following is the graph of variation of acceleration with respect to time:

3.14. Give examples of a one-dimensional motion where
a) the particle moving along positive x-direction comes to rest periodically and moves forward
b) the particle moving along positive x-direction comes to rest periodically and moves backwardπ
Answer:
When an equation has sine and cosine functions, the nature is periodic.
a) When the particle is moving in positive x-direction, it is given as t > sin t
When the displacement is as a function of time, it is given as x(t) = t – sin t
When the equation is differentiated with respect to time, we get
Velocity v(t) = dx(t)/dt = 1 – cos t
Differentiating the above equation again with respect to time, we get
Acceleration, a(t) = dv/ dt = sin y
When t = 0, x(t) = 0
When t = π, x(t) = π > 0
When t = 0, x(t) = 2 π > 0
b) The equation is given as
x(t) = sin t
v = (d/dt)x(t) = cos t
a = dv/dt = -sin t
At t = 0, x = 0, v = 1 and a = 0
At t = π/2, x = 1, v = 0 and a = -1
At t = π, x = 0, v = -1, and a = 0
At t = 3 π/2, x = -1, v = 0 and a = 1
Therefore, it can be said that when the particle is moving along the positive x-direction, the particle comes to rest periodically and moves backward. When the displacement and velocity is involved, that is sin t and cos t, the equations are represented periodic in nature.
3.15. Give example of a motion where x>0, v<0, a>0 at a particular instant.
Answer:
Let the motion be represented as:
x(t) = A + Be– γ t
Let A>B and γ >0
Velocity is x(t) = dx/dt = -Be– γ t
Acceleration is a(t) = dx/dt = B γ 2e– γ t
Therefore, it can be said that x(t) > 0, v(t) < 0, and a>0
3.16. An object falling through a fluid is observed to have acceleration given by a = g – bv where g = gravitational acceleration and b is constant. After a long time of release, it is observed to fall with constant speed. What must be the value of constant speed?
Answer:
The concept used in this question will be based on the behaviour of a spherical object when it is dropped through a viscous fluid. When a spherical body of radius r is dropped, it is first accelerated and gradually the acceleration comes to zero, attaining a constant velocity which is known as terminal velocity.
Given,
a = g – bv
We know that,
a = dv/dt = 0 for uniform motion
g = gravitational acceleration
Therefore, it can be said that as the speed increases, acceleration decreases. When the speed is v0, acceleration will be zero and speed remains constant.
Therefore, a = g – bv0 = 0
v0 = g/b
Short Answers
3.17. A ball is dropped and its displacement vs time graph is as shown in the figure where displacement x is from the ground and all quantities are positive upwards.

a) Plot qualitatively velocity vs time graph
b) Plot qualitatively acceleration vs time graph
Answer:
a) At t=0 and v=0 , v-t graph is:

b) At x = 0, a-t graph is:

3.18. A particle executes the motion described by x(t) = x0 (1 – e-γt) where t ≥ 0, x0 > 0
a) Where does the particles start and with what velocity?
b) Find maximum and minimum values of x(t), v(t), a(t). Show that x(t) and a(t) increase with time and v(t) decreases with time.
Answer:
a) x(t) = x0 (1 – e-γt)
v(t) = dx(t)/dt = +x0 γ e-γt
a(t) = dv/dt = x0 γ2 e-γt
v(0) = x0 γ
b) x(t) is minimum at t = 0 since t = 0 and [x(t)]min = 0
x(t) is maximum at t = ∞ since t = ∞ and [x(t)]max = e-γt = ∞
v(t) is maximum at t = 0 since t = 0 and v(0) = x0γ
v(t) is minimum at t = ∞ since t = ∞ and v(∞) = 0
a(t) is maximum at t = ∞ since t = ∞ and a(∞) = 0
a(t) is minimum at t = 0 since t = 0 and a(0) = -x0 γ2
3.19. A bird is tossing between two cars moving towards each other on a straight road. One car has a speed of 18 m/h while the other has the speed of 27 km/h. The bird starts moving from first car towards the other and is moving with the speed of 36 km/h and when the two cars were separated by 36 km. What is the total distance covered by the bird? What is the total displacement of the bird?
Answer:
The relative speed of the cars = 27 + 18 = 45 km/h
When the two cars meet together, time t is given as
t = distance between cars/relative speed of cars
= 36/(27+18)
t = 4/5 h
Therefore, distance covered by the bird in 4/5 hours = (36)(4/5) = 28.8 km
3.20. A man runs across the roof-top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is of a lower height than the first. If his speed is 9 m/s, the distance between the two buildings is 10 m and the height difference is 9 m, will he be able to land on the next building?
Answer:
For a free fall at 9m, the horizontal distance covered by the man should be at least 10 m.

u = 0
a = 10 m/s2
s = 9 m
t = t
s = ut + 1/2 at2
Substituting the values, we get
t = √9/3 = 3/√5 sec
The horizontal distance covered by the person,
vt = (9)( 3/√5) = 12.07 m
Therefore, 12.07 m is the distance covered during a free fall of 9 m.
Therefore, when the free fall is 10 m it is 12.07-10 = 2.07 m
3.21. A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
Answer:
V = v1 = ?
U = 0
h = 45 m
a = g
t = t
V = u + at
v1 = 0 + gt
v1 = gt
Therefore, when the ball is thrown upward, v1 = -gt
V = v2
u = 40 m/s
a = g
t = t
V = u + at
v2 = 40 – gt
The relative velocity of the ball in the downward direction is – 40 m/s
But when the speed increases due to acceleration, the relative speed remains 40 m/s
3.22. The velocity-displacement graph of a particle is shown in the figure.

a) Write the relation between v and x.
b) Obtain the relation between acceleration and displacement and plot it.
Answer:
a) Consider the point P(x,v) at any time t on the graph such that angle ABO is θ such that
tan θ = AQ/QP = (v0-v)/x = v0/x0

When the velocity decreases from v0 to zero during the displacement, the acceleration becomes negative.
a = – tan θ = v0/z0 = (v0-v)/x
v0 – v = (v0/z0)x
v = v0(1-x/x0) is the relation between v and x.
b) a = dv/dt = (dv/dt)(dx/dx) = (dv/dx)(dx/dt)
a = -v0/x0
v = -v0/x0
a = (v02x/x02) – (v02/x0)

At x = 0
a = – v02/x0
At a = 0
The points are (0, -v02/x0) and B(x0,0)
Long Answers
3.23. It is a common observation that rain clouds can be at about a kilometre altitude above the ground.
a) If a rain drop falls from such a height freely under gravity, what will be its speed? Also, calculate in km/h
b) A typical rain drop is about 4 mm diameter. Momentum is mass x speed in magnitude. Estimate its momentum when it hits ground.
c) Estimate the time required to flatten the drop.
d) Rate of change of momentum is force. Estimate how much force such a drop would exert on you.
e) Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
Answer:
a) Velocity attained by the rain drop which is falling freely through the height h is:
v2 = u2 – 2g(-h)
As u = 0
v = √2gh = 100√2 m/s = 510 km/h
b) Diameter of the drop, d = 2r = 4 mm
Radius of the drop, r = 2 mm = 2 × 10-3 m
Mass of the drop, m = Vρ = 3.4 × 10-5 kg
Momentum of the rain drop, p = mv = 5 × 10-3 kg.m/s
c) Time required to flatten the drop is the time taken by the drop to reach the ground
t = d/v = 30 ms
d) Force exerted by a rain drop is, F = change in momentum/time = p-0/t = 168 N
e) Radius of umbrella, R = 1/2 m
Area of umbrella = 0.8 m2
No.of drops striking the umbrella, n = 320
Therefore the net force exerted = 54000N
3.24. A motor car moving at a speed of 72 km/h cannot come to a stop in less than 3 s while for a truck this time interval is 5 s. On a highway the car is behind the truck both moving at 72 km/h. The truck gives a signal that it is going to stop at emergency. At what distance the car should be from the truck so that it does not bump onto the truck. Human response time is 0.5 s.
Answer:
For truck, u = 20 m/s
v = 0
a = ?
t = 5s
v = u + at
a = 4 m/s2
For car, t = 3 s
u = 20 m/s
v = 0
a = ac
v = u + at
ac = -20/3 m/s2
Let s be the distance between the car and the truck when the truck gives the signal and t be the time taken to cover the distance.
The human response is 0.5 s and that is the time taken by the car to cover a certain distance with uniform velocity. Therefore, (t-0.5) is the retarded motion of the car.
Velocity of car after time t,
vc = u – at
= 20 – (20/3)(t-0.5)
Velocity of truck after time t,
vt = 20 -4t
The bump between the car and the truck is given as:
20-(20/3)(t-0.5) = 20 – 4t
t = 5/4s
Distance travelled by the truck in time t = 21.875 m
Distance travelled by the car in time t = 23.125 m
The collision between the truck and the car distance = 1.250 m
3.25. A monkey climbs up a slippery pole for 3 seconds and subsequently slips for 3 seconds. Its velocity at time t is given by v(t) = 2t (3 – t); 0<t<3 and v(t) = -(t – 3) ( 6 – t) for 3 < t < 6s on m/s. It repeats this cycle till it reaches the height of 20 m.
a) At what time is its velocity maximum?
b) At what time is its average velocity maximum?
c) At what times is its acceleration maximum in magnitude?
d) How many cycles are required to reach the top?
Answer:
a) For maximum velocity v(t)
dv(t)/dt = 0
Substituting the value for v, we get
t = 1.5 seconds
b) For average velocity = total distance/time taken
Average velocity = 3 m
And the average velocity is maximum when time t = 2.36 sec
c) When the acceleration is maximum in a periodic motion, the time is maximum when the body returns to the mean position when v = 0
v(t) = 6t – 2t2
When t = 3 second, acceleration is maximum
d) Distance covered between 0-3 second
s = 9m
v(t) = -(t-3) (6-t)
ds/dt = (t-3)(t-6)
Integrating the equation from 3 to 6, s = -4.5m
The net distance = 9 – 4.5 = 4.5m
Height of climb in three cycle = (4.5)(3) = 13.5m
The remaining height = 20 -13.5 = 6.5 m
Therefore, no.of cycles is 20 when the height of the pole is 4.
3.26. A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval. The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15m at t = 2s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
Answer:
Let the speed of ball 1 = u1 = 2u m/s
Then the speed of ball 2 = u2 = u m/s
The height covered by ball 1 before coming to rest = h1
The height covered by ball 2 before coming to rest = h2
We know that,
v2 = u2 + 2gh
v2 = 2gh
h = v2/2g
Therefore, h1 = 4u2/2g
h2 = u2/2g
From question, h1 –h2 = 15 m
Therefore,
4u2/2g – u2/2g = 15
u = 10 m/s
h1 = 20 m
h2 = 5 m
And time taken is,
t1 = 2 sec
t2 = 1 sec
| Also Access |
| NCERT Solutions for Class 11 Physics Chapter 3 |
| CBSE Notes for Class 11 Physics Chapter 3 |
Why Opt for BYJU’S
BYJU’S brings you premier study materials, notes, sample papers, important questions, mock tests, textbooks, worksheets and exemplar problems for all chapters of all subjects of Class 11. Keep visiting BYJU’S for the latest CBSE sample papers, previous years’ question papers, etc.


















Comments