Triangle Law of Vector Addition

What is Vector Addition?

Triangle law of vector addition is one of the vector addition laws. Vector addition is defined as the geometrical sum of two or more vectors as they do not follow regular laws of algebra. The resultant vector is known as the composition of a vector.

There are a few conditions that are applicable for any vector addition, they are:

• Scalars and vectors can never be added.
• For any two vectors to be added, they must be of the same nature. Example, velocity should be added with velocity and not with force.

There are two laws of vector addition, they are:

• Triangle law of vector addition
• Parallelogram law of vector addition

What is Triangle Law of Vector Addition?

Triangle law of vector addition states that when two vectors are represented as two sides of the triangle with the order of magnitude and direction, then the third side of the triangle represents the magnitude and direction of the resultant vector.

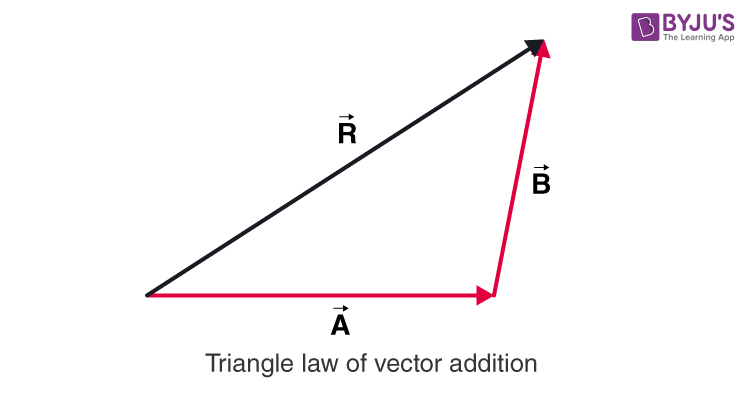
To obtain the resultant vector, we use the following rule:

\(\begin{array}{l}\vec{R}=\vec{A}+\vec{B}\end{array} \)

You may also want to check out these topics given below!

• Vector Addition- Analytical Method
• Addition And Subtraction Of Vectors

Triangle Law of Vector Addition Derivation

Consider two vectors, P and Q, respectively, represented by the sides OA and AB. Let vector R be the resultant of vectors P and Q.

From triangle OCB,

\(\begin{array}{l}OB^{2}=OC^{2}+BC^{2}\end{array} \)

\(\begin{array}{l}OB^{2}=(OA+AC)^{2}+BC^{2}\end{array} \)

(eq.1)

In triangle ACB with ϴ as the angle between P and Q

\(\begin{array}{l}cos\theta =\frac{AC}{AB}\end{array} \)

\(\begin{array}{l}AC=ABcos\theta =Qcos\theta\end{array} \)

\(\begin{array}{l}sin\theta =\frac{BC}{AB}\end{array} \)

\(\begin{array}{l}BC=ABsin\theta =Qsin\theta\end{array} \)

Substituting the values of AC and BC in (eqn.1), we get

\(\begin{array}{l}R^{2}=(P+Qcos\theta )^{2}+(Qsin\theta )^{2}\end{array} \)

\(\begin{array}{l}R^{2}=P^{2}+2PQcos\theta +Q^{2}cos^{2}\theta +Q^{2}sin^{2}\theta\end{array} \)

\(\begin{array}{l}R^{2}=P^{2}+2PQcos\theta +Q^{2}\end{array} \)

therefore,

\(\begin{array}{l} R=\sqrt{P^{2}+2PQcos\theta +Q^{2}}\end{array} \)

The above equation is the magnitude of the resultant vector.

To determine the direction of the resultant vector, let ɸ be the angle between the resultant vector R and P.

From triangle OBC,

\(\begin{array}{l}tan\phi =\frac{BC}{OC}=\frac{BC}{OA+AC}\end{array} \)

\(\begin{array}{l}tan\phi =\frac{Qsin\theta }{P+Qcos\theta }\end{array} \)

therefore,

\(\begin{array}{l} \phi =tan^{-1}(\frac{Qsin\theta }{P+Qcos\theta })\end{array} \)

Above equation is the direction of the resultant vector.

Frequently Asked Questions – FAQs

Q1

What is the meaning of a vector quantity?

A vector quantity is a quantity that has both magnitude as well as a distinct direction.

Q2

What is the meaning of a scalar quantity?

A scalar quantity is a quantity that has only magnitude.

Q3

What is vector addition?

Vector addition is stated as the physical sum of multiple vectors as they do not follow conventional laws of algebra. The resultant vector is called the composition of a vector.

Q4

What are the two laws of vector addition?

Parallelogram law and triangle laws of vector addition are the two fundamental laws of vector addition.

Q5

What are the conditions that are necessary for vector addition?

For any two vectors to be added, they must be identical in nature. For example, velocity should be added with velocity and not with force.

Q6

Write some examples of scalar quantities.

Density, volume, speed, time, energy, and mass are some of the most familiar examples of scalar quantities.

Q7

Write some examples of vector quantities.

Velocity, displacement, force, weight, and acceleration are some of the most common examples of vector quantities.

Stay tuned with BYJU’S to learn more interesting topics with engaging videos!

Watch the video and understand how to represent the equation of a line in three-dimensional space using vector notations.