What is the Circumcenter of a Triangle?
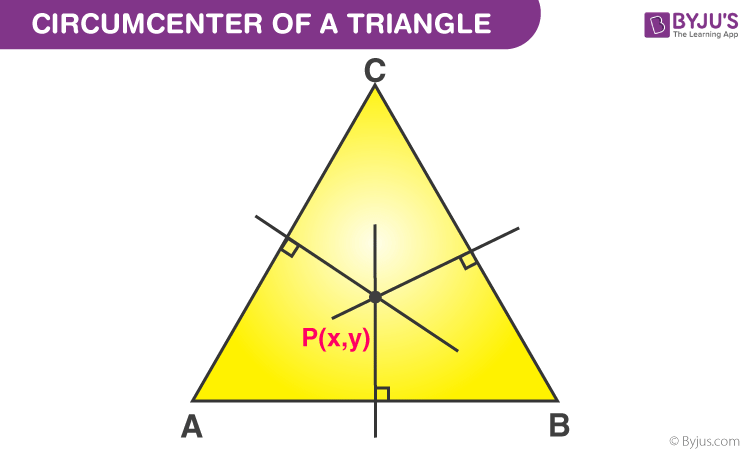
The circumcenter of a triangle is defined as the point where the perpendicular bisectors of the sides of that particular triangle intersect. In other words, the point of concurrency of the bisector of the sides of a triangle is called the circumcenter. It is denoted by P(X, Y). The circumcenter is also the centre of the circumcircle of that triangle and it can be either inside or outside the triangle.
Circumcenter Formula
| P(X, Y) = [(x1 sin 2A + x2 sin 2B + x3 sin 2C)/ (sin 2A + sin 2B + sin 2C), (y1 sin 2A + y2 sin 2B + y3 sin 2C)/ (sin 2A + sin 2B + sin 2C)] |
Here,
- A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of the triangle and A, B, C are their respective angles.
Method to Calculate the Circumcenter of a Triangle
Steps to find the circumcenter of a triangle are:
- Calculate the midpoint of given coordinates, i.e. midpoints of AB, AC, and BC
- Calculate the slope of the particular line
- By using the midpoint and the slope, find out the equation of the line (y-y1) = m (x-x1)
- Find out the equation of the other line in a similar manner
- Solve two bisector equations by finding out the intersection point
- Calculated intersection point will be the circumcenter of the given triangle
Finding Circumcenter Using Linear Equations
The circumcenter can also be calculated by forming linear equations using the distance formula. Let us take (X, Y) be the coordinates of the circumcenter. According to the circumcenter properties, the distance of (X, Y) from each vertex of a triangle would be the same.
Assume that D1 be the distance between the vertex (x1, y1) and the circumcenter (X, Y), then the formula is given by,
D1= √[(X−x1)2+(Y−y1)2]
D2= √[(X−x2)2+(Y−y2)2]
D3= √[(X−x3)2+(Y−y3)2]
Learn More: Distance Between Two Points
Now, since D1=D2 and D2=D3, we get
(X−x1)2 + (Y−y1)2 = (X−x2)2 + (Y−y2)2
From this, two linear equations are obtained. By solving the linear equations using substitution or elimination method, the coordinates of the circumcenter can be obtained.
Properties of Circumcenter
Some of the properties of a triangle’s circumcenter are as follows:
- The circumcenter is the centre of the circumcircle
- All the vertices of a triangle are equidistant from the circumcenter
- In an acute-angled triangle, circumcenter lies inside the triangle
- In an obtuse-angled triangle, it lies outside of the triangle
- Circumcenter lies at the midpoint of the hypotenuse side of a right-angled triangle
How to Construct Circumcenter of a Triangle?
The circumcenter of any triangle can be constructed by drawing the perpendicular bisector of any of the two sides of that triangle. The steps to construct the circumcenter are:
- Step 1: Draw the perpendicular bisector of any two sides of the given triangle.
- Step 2: Using a ruler, extend the perpendicular bisectors until they intersect each other.
- Step 3: Mark the intersecting point as P which will be the circumcenter of the triangle. It should be noted that, even the bisector of the third side will also intersect at P.
Learn More:
Example Question Using Circumcenter Formula
Question: Find the coordinates of the circumcenter of a triangle ABC with the vertices A = (3, 2), B = (1, 4) and C = (5, 4)?
Solution:
- Method 1:
Let, (x, y) be the coordinates of the circumcenter.
D1 be the distance from the circumcenter to vertex A
D2 be the distance from the circumcenter to vertex B
D3 be the distance from the circumcenter to vertex C
Given : (x1 , y1) = (3, 2) ; (x2 , y2) = (1, 4) and (x3 , y3) = (5, 4)
Using distance formula, we get
D1= √[(X−x1)2+(Y−y1)2]
D2= √[(X−x2)2+(Y−y2)2]
D3= √[(X−x3)2+(Y−y3)2]
Since D1= D2 = D3 .
D1= D2 gives,
(x – 3)2 + (y − 2)2 = (x − 1)2 + (y − 4)2
⇒ x2 − 6x + 9 + y2 + 4 − 4y = x2 + 1 – 2x + y2 – 8y + 16
⇒ -6x – 4y + 13 =-2x – 8y + 17
⇒ -4x + 4y = 4
⇒ -x + y = 1 ———–(1)
D1= D3 gives,
(x – 3)2+(y − 2)2 = (x − 5)2 + (y – 4)2
⇒ x2 − 6x + 9 + y2 + 4 − 4y = x2 + y2 − 10x – 8y + 25 + 16
⇒ -6x – 4y + 13 = -10x – 8y + 41
⇒ 4x + 4y = 28
Or, x + y = 7 ————–(2)
By solving equation (1) and (2), we get
2y = 8
Or, y = 4
Now, substitute y = 4 in equation(1),
⇒ -x + 4 = 1
⇒ -x = 1 – 4
⇒ -x = -3
Or, x = 3
Therefore, the circumcenter of a triangle is (x, y) = (3, 4)
- Method 2:
Given points are,
A = (3, 2),
B = (1, 4),
C = (5, 4)
To find out the circumcenter we have to solve any two bisector equations and find out the intersection points.
So, mid point of AB = [(3 + 1)/2, (2 + 4)/2] = (2, 3)
Slope of AB = [(4−2)/(1−3)] = -1
The slope of the bisector is the negative reciprocal of the given slope.
So, the slope of the perpendicular bisector = 1
Equation of AB with slope 1 and the coordinates (2, 3) is,
(y – 3) = 1(x – 2)
x – y = -1………………(1)
Similarly, for AC
Mid point of AC = [(3 + 5)/2, (2 + 4)/2] = (4, 3)
Slope of AC = [(4−2)/(5−3)] = 1
The slope of the bisector is the negative reciprocal of the given slope.
So, the slope of the perpendicular bisector = -1
Equation of AC with slope -1 and the coordinates (4, 3) is,
(y – 3) = -1(x – 4)
y – 3 = -x + 4
x + y = 7………………(2)
By solving equation (1) and (2),
(1) + (2) ⇒ 2x = 6;
Or, x = 3
Substitute the value of x in to (1)
3 – y = -1
y = 3 + 1 = 4
Thus, the circumcenter is (3, 4).
Frequently Asked Questions
What is Circumcenter?
The circumcenter is the intersection point of the perpendicular bisectors of sides of a triangle. It is the centre of a triangle’s circumcircle.
How to Find the Circumcenter of a Triangle?
To find the circumcenter of any triangle, draw the perpendicular bisectors of the sides and extend them. The point at which the perpendicular intersects each other will be the circumcenter of that triangle.
Does Every Triangle have a Circumcenter?
Yes, every triangle has a circumcenter. The circumcenter can be either inside the triangle or outside.
Where is the Circumcenter of an Obtuse Angled Triangle and a Right Angled Triangle?
The circumcenter of an obtuse-angled triangle is outside the triangle. For a right-angled triangle, the circumcenter lies on the hypotenuse.

Comments