What Is Alternating Current?
An alternating current can be defined as a current that changes its magnitude and polarity at regular intervals of time. It can also be defined as an electrical current that repeatedly changes or reverses its direction opposite to that of Direct Current or DC, which always flows in a single direction as shown below.
Download Complete Chapter Notes of Alternating Current
Download Now
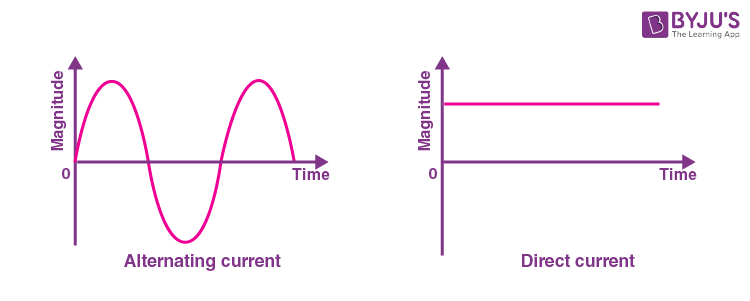
From the graph, we can see that the charged particles in AC tend to start moving from zero. It increases to a maximum and then decreases back to zero completing one positive cycle. The particles then reverse their direction and reach the maximum in the opposite direction after which AC again returns to the original value completing a negative cycle. The same cycle is repeated again and again.
Alternating currents are also accompanied usually by alternating voltages. Besides, alternating current is also easily transformed from a higher voltage level to a lower voltage level.
Alternating Current Production
Alternating current can be produced or generated by using devices that are known as alternators. However, alternating current can also be produced by different methods where many circuits are used. One of the most common or simple ways of generating AC is by using a basic single coil AC generator, which consists of two-pole magnets and a single loop of wire having a rectangular shape.
In this setup, the AC generator follows Faraday’s principle of electromagnetic induction where it converts mechanical energy into electrical energy.
Meanwhile, AC is supplied to pieces of equipment using 3 wires. They are as follows;
- Power is transmitted by the hot wire.
- The neutral wire which is connected to the earth provides a return path for the current in the hot wire.
- The third wire that is also connected to the earth is linked to the metallic parts of the equipment to mainly eliminate electric shock hazards.
Application of Alternating Current
AC is the form of current that is mostly used in different appliances. Some of the examples of alternating current include audio signal, radio signal, etc. An alternating current has a wide advantage over DC as AC is able to transmit power over large distances without great loss of energy.
AC is used mostly in homes and offices mainly because the generating and transporting of AC across long distances is a lot easier. Meanwhile, AC can be converted to and from high voltages easily using transformers. AC is also capable of powering electric motors that further convert electrical energy into mechanical energy. Due to this, AC also finds its use in many large appliances like refrigerators, dishwashers and many other appliances.
Alternating Current Waveform
Before we learn more about this topic, let us quickly understand a few key terms.
- The time interval between a definite value of two successive cycles is the period.
- The number of cycles or number of periods per second is frequency.
- The maximum value in both directions is the amplitude.
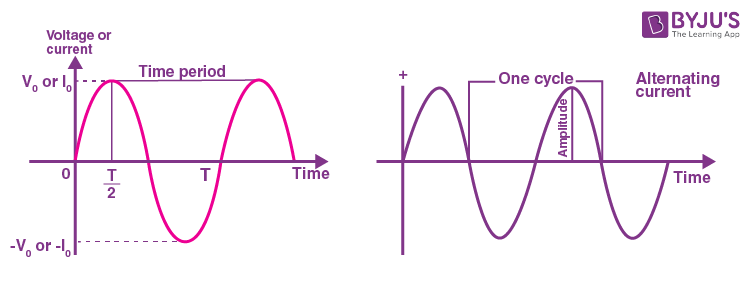
The normal waveform of AC in most of the circuits are sinusoidal in nature in which the positive half period corresponds with the positive direction of the current and vice-versa. In addition, a triangular or square wave can also be used to represent the alternating current waveform.
Audio amplifiers that deal with analogue voice or music signals produce irregular AC waves. Some electronic oscillators produce square or sawtooth waves.
Also Read: Differences Between AC and DC
Average Value of AC
The average value is usually defined as the average of the instantaneous values of alternating current over a complete cycle. The positive half cycle of asymmetrical waves such as a sinusoidal voltage or current waveform will be equal to the negative half cycle. This implies that the average value after the completion of a full cycle is equal to zero.
Since both the cycles do some work, the average value is obtained by avoiding the signs. Therefore, the average value of alternating quantities of sinusoidal waves can be considered by taking the positive cycle only.
RMS Value of AC Wave
RMS value is defined as the square root of means of squares of instantaneous values. It can also be described as the amount of AC power that generates the same heating effect as an equivalent DC power.
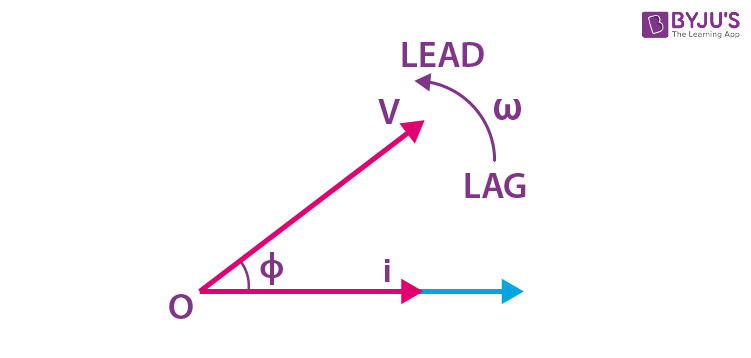
Phasor Diagrams
The phasor diagram is used to determine the phase relationships between two or more sine waves propagating with the same frequency. Here, we use the terms “lead”, “lag” and also “in-phase”, “out-of-phase” to indicate the relation between one waveform with the other.
Phasor diagrams will be of the form:
AC Circuit Containing Resistance Only
The pure resistive AC circuit contains only pure resistance of R ohms. There will be no effect of inductance and capacitance in this circuit. The alternate current and voltage move along both directions as backwards and forwards. Therefore, current and voltage follow a shape of sine.
In a purely resistive circuit, the power is dissipated by the resistors and the phase of both voltage and current remains the same. This means that the voltage and current reaches a maximum value at the same time.
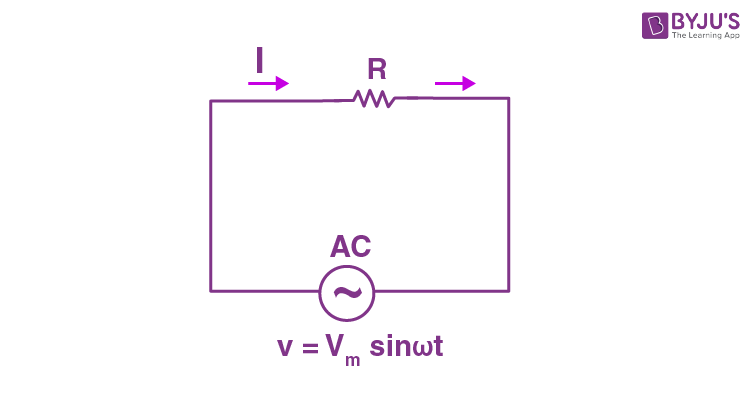
Let the supply voltage be,
v = Vmsinωt ……(1)
The instantaneous value of current flowing through the given circuit is,
i = v / R = Vm / R sinωt ……(2)
From equation (2), the value of current be maximum at t = 900, so sin t =1
Then, the instantaneous value of current will be,
i = Imsinωt ……(3)
So, by observing the equation (1) and (3), it is clear that there is no phase difference between the applied voltage and current flowing through the circuit. Meaning, phase angle between voltage and current is zero.
Hence, in a pure resistive ac circuit, the current is in phase with the voltage.
This can be expressed in a waveform as,
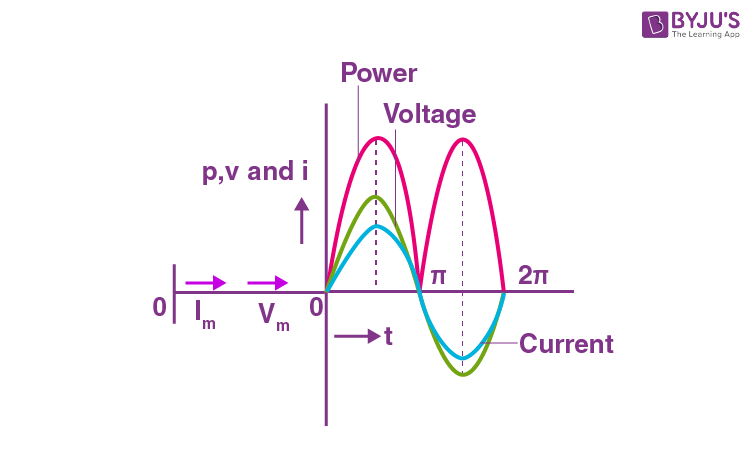
AC Circuit Containing Inductance Only
This type of circuit contains only inductance. There will not be any effect of resistance and capacitance in this circuit. Here, the current will lag behind the voltage by an angle of 900.
The circuit will be,
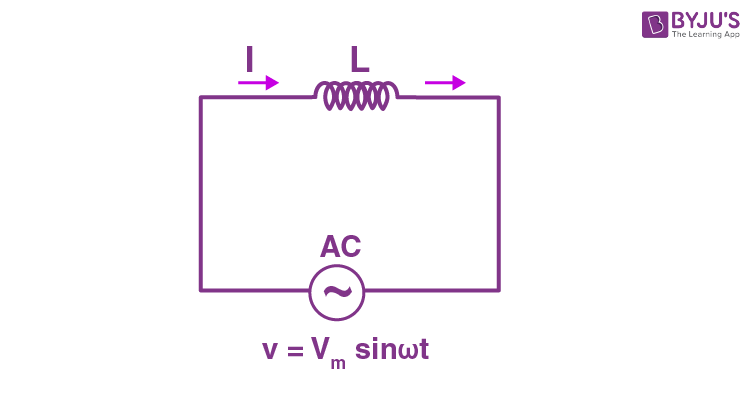
The inductor will reserves electrical energy in the magnetic field when current flows through it. When this current changes, the time-varying magnetic field causes emf which opposes the flow of current. This opposition to the flow of current is known as inductive reactance.
Let the voltage applied to the circuit be,
v = Vmsinωt ……(1)
The emf induced in the inductor will be,
E = -L x di / dt
This emf induced in a circuit is equal and opposite to applied voltage.
v = -e ……(2)
Putting the value of e in (2) we get,
v = (-L x di / dt)
Or
Vmsinωt = L x di / dt
Or
di = Vm / L sinω dt ……(3)
Integrating both sides, we get,
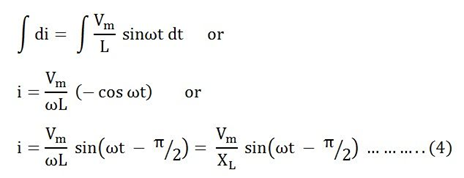
Here,
Inductive reactance is XL = ωL
The value of current will be maximum if sin (ωt – π/2) = 1
Therefore,
Im = Vm / XL ……(5)
Apply the value of Im from (5) and put in (4)
We get,
i = Im sin (ωt – π / 2)
This implies that the current in pure inductive ac circuits lags the voltage by 900.
This can be expressed in a waveform as,
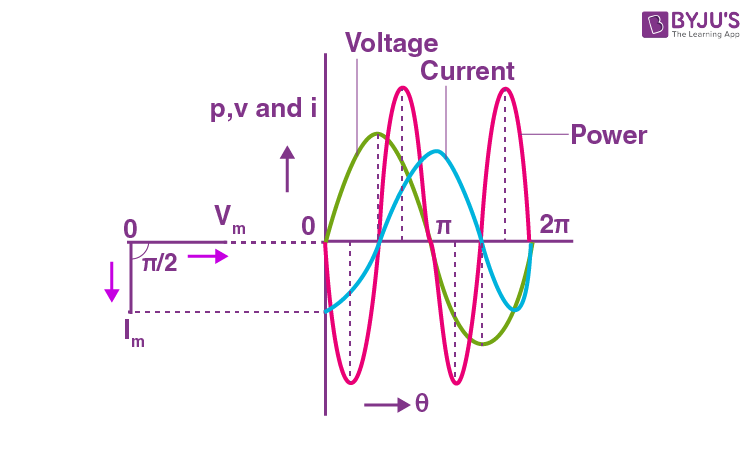
If the voltage and current are at their peak value as a positive value, the power will also be positive. Similarly, if the voltage and current are at a negative peak then the power will be negative. This is because of the phase difference between them.
AC Circuit Containing Capacitor Only
This type of circuit includes a pure capacitor only. It will not affect the properties of resistance and inductance. The capacitor will store electric power in the electric field. This is known as capacitance.
The electric field is developed across the plates of the capacitor when a voltage is applied across the capacitor. Also, there will not be any current flows between them.
The circuit will be,
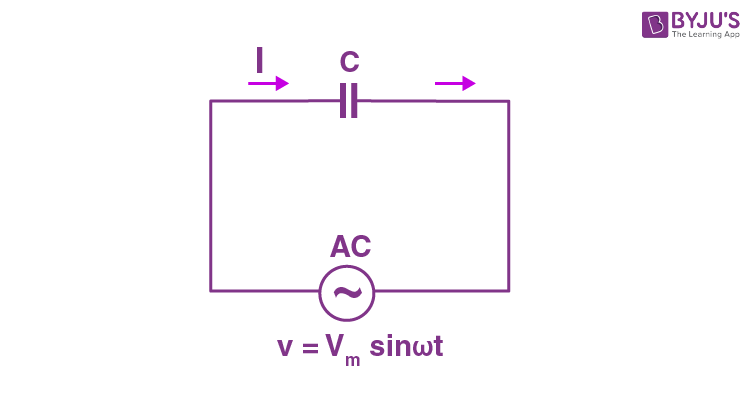
As we know, a capacitor includes two insulating plates which are separated by a dielectric medium. Usually, a capacitor works as a storage device and it gets charged if the supply is on and it gets discharged if the supply is off.
Let the voltage applied to the circuit be,
v = Vmsinωt ……(1)
Charge of the capacitor is,
q = Cv ……(2)
Then, current flow through the circuit will be,
i = dq / dt
Substituting the value of q in the above equation we get,
i = d (Cv) / dt ……(3)
Now substitute the value of v in (3), we get,
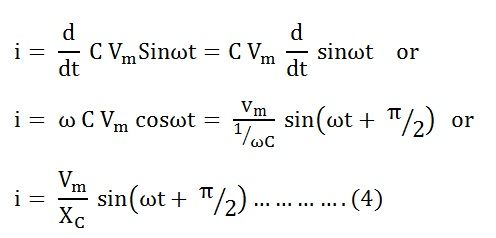
Where XC = 1/C which is capacitive inductance.
The value of current will be maximum if sin(ωt + π/2) = 1.
Then, the maximum value of current,
Im = Vm / XC
Substituting the value of Im in (4) we get,
i = Im sin (ωt + π / 2)
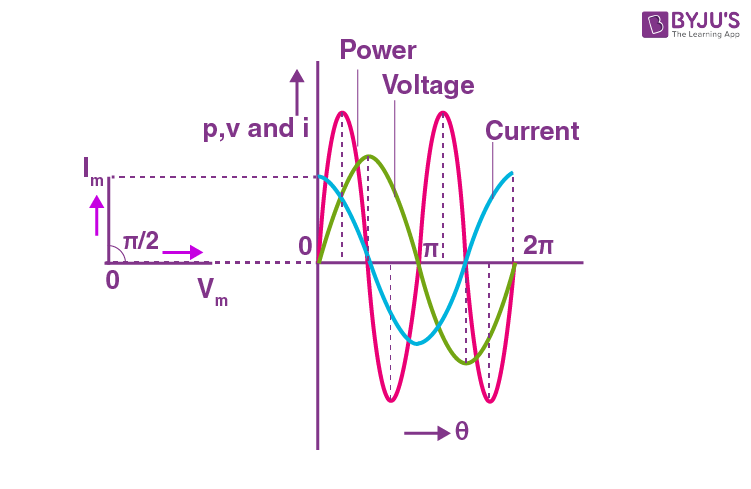
This implies that the current flowing through the capacitor leads the voltage by 900.
This can be expressed in a waveform as,
Alternating Current vs Direct Current
| Alternating Current | Direct Current |
| It is safer to transfer over longer distances and helps to maintain electric power. | Cannot be transferred over very long distances. It has a tendency to lose electric power. |
| AC can change its direction during electric flow. | It does not change its direction during flow and remains constant. |
| The frequency of AC depends from country to country. | The frequency of DC is zero. |
| An alternator is used to generate AC. | DC current is generated by generators, photovoltaic cells and batteries. |
| Electrons keep changing their directions. It can be either backward or forward. | Electrons move only in the forward direction. |
| Load on AC can be inductive, capacitive or resistive. | Load on DC is always resistive. |
Alternating Current Notes and Revision

Alternating Current – Top 10 Most Important & Expected JEE Main Questions

Alternating Current Important JEE Main Questions

Frequently Asked Questions on Alternating Current
Define the period of alternating current.
The period of alternating current is the time taken by it to complete one cycle.
Define the frequency of the alternating current.
The frequency of AC is the number of cycles completed by the alternating current in one second.
Give one method of generating sinusoidal alternating current.
A sinusoidal AC can be generated by rotating a coil in a uniform magnetic field at a constant rate.
What is the RMS value of an AC?
The RMS value of an AC is the square root of the mean of the squares of the instantaneous values taken over a complete cycle.
What are the advantages of AC over DC current?
Alternating current can be stepped up or stepped down using a transformer.
Using electronic supply units, AC can be converted into DC.
Alternating current devices are more durable since power dissipation is less.
Transmission of electrical power is more efficient and economical in the form of AC.
Define the period of alternating current.
The period of alternating current is the time taken by it to complete one cycle.
What is the mean value of an AC?
The mean value of AC is the mean or average of the instantaneous values of AC taken over half a cycle.

Comments