The Kerala SSLC Class 10 Maths Important Questions are prepared keeping in mind the need to give an overview of the major topics and concepts under Kerala Board Class 10 maths to the students. Many feel that maths is a tough subject and it requires a lot of practice if they want to excel in the subject. These important questions prepared as per the SSLC syllabus can help students to get the practice and gain more confidence. It definitely gets better with practice. If the students solve more papers they are more liable to grasp the concepts more easily.
The questions compiled here is done after analyzing the questions that came in the Kerala SSLC Previous Year Papers. We have taken the most important questions, those of which we feel are liable to be repeated again for the upcoming boards. These questions will also give the students an idea about the type of questions asked and this helps them to prepare for the exams better. Meanwhile, take a look at the important questions of class 10 mathematics, which we have compiled here:
Download Kerala SSLC Class 10 Maths important Question PDF
KBPE Class 10th Maths Important Questions & Answers
Question 1: In the figure given below OABC is a rectangle and its breadth is 3. Write the coordinates of the vertices B and C.

Solution:
The coordinates of the vertex B are (6, 3) and vertex C are (0, 3).
Question 2: The algebraic form of an arithmetic sequence is 5n + 3.
[a] What is the first form of sequence?
[b] What will be the remainder if the terms of the sequences are divided by 5?
Solution:
[a] The given arithmetic sequence is 5n + 3.To obtain the first term of the sequence, put n = 1.
a = 5 (1) + 3 = 8
[b] The remainder obtained when the terms of the sequence are divided by 5 is given byα0 = 5 (0) + 3 = 3
∴ Remainder = 3 when the terms of sequence are divided by 5.
Question 3: In the figure, ‘O’ is the centre of the circle and A, B, C, D, E are the points on it.

∠EAB = 120⁰, ∠EPD = 100⁰. Write the measures of ∠EDB, ∠ECB and ∠DBC.
Solution:
ABCDE is a cyclic quadrilateral.
∠EDB + ∠EAB = 180o
120o + ∠EDB = 180o
∠EDB = 60o
ABCE is a cyclic quadrilateral.
∠EAB + ∠ECB = 180o
120o + ∠ECB = 180o
∠ECB = 60o
∠BPE = ∠DPE [vertically opposite angles]
∠BPE = 100o
In triangle BPC,
∠BPC + ∠BCP + ∠PBC = 180o
100o + 60o + ∠PBC = 180o
∠PBC = 180o – 160o
∠PBC = 20o
∠DBC = 20o [same arc angles]
Question 4: Draw a circle of 3cm. Mark a point 7cm away from its centre. Draw tangents to the circle from this point.
Solution:

Steps of construction:
- Draw a circle of 3cm radius and O as its centre.
- From the centre, mark OP = 7cm.
- Draw a perpendicular bisector of the line OP such that it meets at M.
- Draw a circle with radius OM and cut the circle at Q and R.
- Joint PR and PQ.
- Hence, PR and PQ are tangents.
Question 5: P(x) = x³ + ax² – x + b and
[a] Find the relation between a and b for x-1 to be a factor of P(x).
[b] Find the relation between a and b for x-2 to be a factor of P(x).
[c] Find a and b so that both x-1 and x-2 are factors of P(x).
Solution:
Given P(x) = x3 + ax2 – x + b
[a] x – 2 is a factor of P(x)P(1) = 0
P(1) = (1)3 + a × (1)2 − 1 + b = 0
= 1 + a − 1 + b = 0
a + b = 0
[b] x – 2 is a factor of P(x)P(2) = 0
P(2) = 23 + a × 22 − 2 + b = 0
= 8 + 4a – 2 + b = 0
= 4a + b = – 6
[c] We have, a + b = 0 and 4a + b = – 6 .Solve these two equations, a = – 2 and b = 2.
Question 6: A circle with centre (3, 4) passes through the origin.
[a] What is the radius of the circle?
[b] If a point in the circle is (x,y), write the relation between x, y?
[c] Check if the point (-2, 1) lies on this circle?
Solution:

Given , center (3, 4) ; Origin (0, 0).
[a] Radius (r) = √x2 + y2= √32 + 42
= √9 + 16
= √25
= 5
[b] Equation of the circle = (x − a)2 + (y − b)2 = r2(x − 3)2 + (y − 4)2 = 52
⇒ x2 − 6x + 9 + y2 −8y + 16 = 25
⇒ x2 + y2 −6x − 8y + 25 − 25 = 0
⇒ x2 + y2 − 6x − 8y = 0 is the equation of the circle.
[c] (- 2, 1) , substitute this value in the equation of the circle, we get,(−2)2 + (1)2 − 6 × −2 −8 × 1 = 0
4 + 1 + 12 – 8 = 0
17 – 8 = 0
9 ≠ 0
AC > radius of the circle.
Hence, the point (-2, 1) lies outside the circle.
Question 7: A boy saw the top of a building under construction at an elevation of 30⁰. The completed building was 12 meters higher and the boy saw its top at an elevation of 60⁰ from the same spot.
[a] Draw a rough figure based on the given details.
[b] What is the height of the building?
[c] What is the distance between the building and the boy?
Solution:
[a]
In triangle ABD, AD / AB = tan 600
AB = AD / tan 600
⇒ AB = x + 12 / √3 …………. (1)
In triangle ABC,
AC / AB = tan 300
⇒ AB = AC / tan 300
⇒ AB = x / [1 / √3]
= x √3 ………. (2)
Comparing equations (1) and (2),
[x + 12] / [√3] = x √3⇒ 3x = x + 12
⇒ 3x – x = 12
⇒ 2x = 12
x = 6
Hence, the height of the building = 6 + 12 = 18 m.
[c] Consider the equation (2), AB = √3 x= √3 × 6
= 1. 73 × 6
= 10.38m
Distance between the building and the boy = 10.38m.
Question 8: Cards marked with numbers 1, 2, 3, 4, …………………, 20 are well shuffled and a card is drawn at random. What is the probability that the number on the card is a:
[a] prime number?
[b] divisible by 3?
[c] a perfect square?
Solution:
Total numbers = 20
[a] The prime numbers are 2, 3, 5, 7, 11, 13, 17, 19Favourable cases = 8
The probability of getting a prime number = 8 / 20 = 2 / 5
[b] The numbers divisible by 3 are 3 ,6 ,9 ,12 ,15 ,18Favourable cases = 6
Probability of getting a number divisible by 3 = 6 / 20 = 3 / 10
[c] The perfect squares are 1, 4, 9, 16Favourable cases = 4
Probability of getting a perfect square number = 4 / 20 = 1 / 5
Question 9: A person bought a certain number of pens for Rs. 800. If he had bought 4 pens more for the same money, he would have paid 10 less for each pen. How many pens did he buy?
Solution:
Let a person buy x number of pens.
One pen costs 800 / x.
If he buys 4 more pens means (x + 4) pens then one pen will cost (800 / x – 10).
So total money required to buy x + 4 pens is (x + 4) * (800 / x – 10)
= 800 + 3200 / x – 10x – 40
Multiplying above by x,
– 10x2 + 760x + 3200
x = – 4 and x = 80
80 pens are bought by the person.
Question 10: Prove that [cos2 a + tan2 a – 1] / [sin2 a] = tan2 a.
Solution:
[cos2 a + tan2 a – 1] / [sin2 a]= [cos2 a / sin2 a] + [tan2 a / sin2 a] – [1 / sin2 a]
= cot2 a + sec2 a – cosec2 a
= [cos2 a – 1] / sin2 a + (1 / cos2 a)
= 1 + sec2 a
= tan2 a
Question 11: A conical tent is to accommodate 11 persons. Each person must have 4 sq. m of the space on the ground and 20 cubic metres of air to breath. Find the height of the cone.
Solution:
Area of the base = 11 × 4 = 44 m2 and volume of the cone = 11 × 20 = 220 m3
[1 / 3] × πR2h = 220 m3 ….(i)Area of the base = πR2
πR2 = 44
R2 = 44 / 22 × 7
R2 = 14
R = √14 ……(ii)
By equation (i) and (ii),
[1 / 3] × [22 / 7] × √14 × √14 × h = 220h = 220 × [3 / 22 × 2]
h = 30 / 2 = 15 cm
Question 12: Mohan has a recurring deposit in a bank, where he deposited Rs.2500 per month for 2 years. If he gets Rs. 66,250 at the time of maturity, find:
[a] The interest paid by the bank
[b] The rate of interest
Solution:
I = MV – nx
I = 66250 – (2500*24)
I = 66250 – 60000
I = 6,250
6250 = 2500 * 24 * 25 * R / 2 * 12 * 100
6250 = 625R
R = 10%
Question 13: The weekly wages of 40 workers in a small factory is given below. If the mean weekly wage is Rs. 145, find the value of a and b.
| Daily wages | 80 – 100 | 100 – 120 | 120 – 140 | 140 – 160 | 160 – 180 |
| Number of workers | 4 | 6 | a | b | 18 |
Solution:
| Daily wages | 80 – 100 | 100 – 120 | 120 – 140 | 140 – 160 | 160 – 180 |
| Number of workers | 4 | 6 | a | b | 18 |
| Midpoint | 90 | 110 | 130 | 150 | 170 |
| xifi | 360 | 660 | 130a | 150b | 3060 |
Mean = 145
n = 40
4 + 6 + a + b + 18 = 40
a + b = 40 – 28
a + b = 12
a = b – 12 —- (1)
Mean = ∑fx / ∑fi
145 = [360 + 660 + 130a + 150b + 3060] / 40
5800 = 4080 + 130a + 150b
1720 = 130a + 150b
1720 = 130 [b – 12] + 150b
1720 = 130b – 1560 + 150b
1720 + 1560 = 280b
3280 / 280 = b
b = 12
a = b – 12
a = 12 – 12 = 0
Question 14: Find the value of x, given that B² = A, where .
.
Solution:

Question 15: Construct a △ABC in which AB = AC = 5cm and BC = 3.2cm. Using a ruler and a compass only draw the reflection A’BC of △ABC in BC. Draw lines of symmetry of the figure ABA’C.
Solution:
AB = AC = 5 cm and BC = 3.2 cm
Step 1: Draw a line BC = 3.2 cm
Step 2: Take the radius of 5 cm and centre as B and C, draw two arcs that intersect at A. The triangle ABC is obtained.
Step 3: The radius of 5 cm and centre B and C are taken, draw two arcs opposite side of point A, both the arcs intersect at A, The reflection of triangle ABC is obtained.

Question 16: [a] Write the 6th term of the arithmetic sequence 1, 25, 49, 73, 97 …..
[b] How many perfect square terms are there in the arithmetic sequence 97, 73, 49 …..?
Solution:
[a] Given an arithmetic sequence is 1, 25, 49, 73, 97 , ………….First term (f) = 1
d = 25 – 1 = 24.
T6 = a + (n – 1)d
6th term = f + 5d
⇒ 1 + 5 × 24
⇒ 1 + 120 = 121
[b] Given an arithmetic sequence is 97, 73, 49, ……….The perfect square numbers are 1, 4, 9, 16, ……….
Hence the given sequence is 97, 73, 49, 25, 1.
From the above sequence, the perfect square numbers are 49, 25, and 1.
∴ The number of perfect square terms are 3.
Question 17: In the figure, ∠ABC = 90o, ∠C = ∠D = 45o, AB = 10cm.

[a] What is the length of AC?
[b] What is the radius of the circumcircle of triangle ABC?
[c] What is the radius of the circumcircle of triangle ABD?
Solution:
In right △ ABC, the angles are 450, 450, 900
⇒ 1 : 1 : √2
⇒ AB : BC : AC
⇒ x : x : x √2
⇒ 10 : 10 : 10√2
[a] The length of AC = 10√2 cm. [b] The radius of the circumcircle of △ABC= Half of the hypotenuses AC
= 10 √2 / 2
= 5√2 cm
[c] The radius of the circumcircle of △ABD= Half of the hypotenuses AC
= 10 √2 / 2
= 5√2 cm
Question 18: The figure of a square sheet paper is shown below. Length of one side of the paper sheet is 36cm and AB = 10cm. The shaded portion is cut out and folded into a square pyramid.

[a] What is the length of the base of the pyramid?
[b] What is the slant height of the pyramid?
[c] Find the lateral surface area of the pyramid.
Solution:
Given, Side of the paper sheet = 36cm
AB = 10cm
[a] Base edge of the pyramidAB = 10cm
[b] Slant height of the pyramid= [36 − 10] / 2
= 26 / 2
= 13cm [∵ a + 2l = 36, side of the larger square] [c] Lateral surface area = 2al
= 2 × 10 × 13
= 260 cm2
Question 19: In a school, the total number of students in 10 A division is equal to the number of students in 10 B. One student is to be selected from each division. The number of boys in 10 A is 20. The probability of selecting a boy from 10 A is (2 / 5) and that of class B is (3 / 5).
[a] How many students are there in 10 A?
[b] What is the probability of selecting a girl from 10 A?
[c] How many boys are there in 10 B?
[d] What is the probability of both the selected students being boys?
Solution:
| Class | XA | XB |
| Boys | 20 | 30 |
| Girls | 30 | 20 |
| Total | 50 | 50 |
Given the probability of boys in XA = 2 / 5
Given the probability of boys in XB = 3 / 5
[a] Number of boys in XA= 20 × [5 / 2]
= 50
[b] Probability of girl from XA= 1 − [2 / 5]
= [5 − 2] / 5
= 3 / 5
[c] Number of boys in X B= 50 × [3 / 5]
= 10 × 3
= 30
[d] Both being boys= [2 / 5] × [3 / 5]
= 6 / 25
Question 20:
[a] If p(x) = x2 – 7x + 13, what is p(3)?
[b] Write the polynomial p(x) – p(3) as the product of two first degree polynomials.
[c] Find the solutions of the equation p(x) – p(3) = 0.
Solution:
[a] Given polynomialp(x) = x2 – 7x + 13
p(3) = 32 − 7 × 3 + 13
= 9 – 21 + 13
= 1
[b] p(x) – p(3) = x2 – 7x + 13 – 1= x2 − 7x + 12
= (x – 3) (x – 4)
Hence the product two first degree polynomial = (x – 3) (x – 4)
[c] p(x) – p(3) = 0x2 – 7x + 12 = 0
⇒ (x – 3) (x – 4) = 0
⇒ (x – 3) = 0 or (x – 4 ) = 0
ie., x = 3 or x = 4.
Hence the solution is x = 3 and 4.
Question 21: [i] If C (-1, k) is a point on the line passing through the points A (2, 4) and B (4, 8) which number is k?
[ii] What is the relation between the x coordinate and the y coordinate of any point on this line?
Solution:
[i]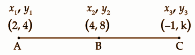
Points A, B and C are collinear.
Area of triangle ABC = 0
(1 / 2) (x1 [y2 – y3] + x2 [y3 – y1] + x3 [y1 – y2])
|2 (8 – k) + 4 (k – 4) + (-1) (4 – 8)| = 0
16 – 2k + 4k – 16 – 4 + 8 = 0
2k = -4
k = -2
[ii]
Area of triangle ABP = 0
(1 / 2) (x1 [y2 – y3] + x2 [y3 – y1] + x3 [y1 – y2])
|2 (8 – y) + 4 (y – 4) + (x) (4 – 8)| = 0
16 – 2y + 4y – 16 – 4x = 0
2y – 4x = 0
2y = 4x
y = 2x
2x – y = 0
Question 22: A box contains some green and blue balls. 7 red balls are put into it. Now the probability of getting a red ball from the box is 7 / 24 and that of the blue ball is 1 / 6.
[i] How many balls are there in the box?
[ii] How many of them are blue?
[iii] What is the probability of getting a green ball from the box?
Solution:
Let the number of green balls be x.
The number of blue balls is y.
Number of red balls = 7
Total number of balls = x + y + 7
P (red ball) = 7 / 24
P (blue ball) = 1 / 3
[i] Since P(red ball) = 7 / 24,7 / [x + y + 7] = 7 / 24
24 = x + y + 7
24 – 7 = x + y
17 = x + y —- (1)
P (blue ball) = 1 / 3
y / [x + y + 7] = 1 / 3
3y = x + y + 7
2y = x + 7
-x + 2y = 7 —- (2)
On adding equation (1) and (2),
17 = x + y
-x + 2y = 7
_______
3y = 24
y = 24 / 3
y = 8
Put y = 8 in equation (1),
17 = x + 8
17 – 8 = x
x = 9
Total number of balls = 8 + 9 + 7 = 24
[ii] Number of blue ballsy / 24 = 1 / 3
3y = 24
y = 8
[iii] P (green ball) = x / 24 = 9 / 24 = 3 / 8Question 23: Circle with centre O touches the sides of a triangle at P, Q and R, AB = AC, AQ = 4cm and CQ = 6cm.

[a] What is the length of CP?
[b] Find the perimeter and the area of the triangle.
[c] What is the radius of the circle?
Solution:

CP = 6cm
[b] Perimeter of triangle = 4 + 6 + 6 + 6 + 4 + 6 = 32 cmFor the area of △ABC,
s = [AB + BC + CA] / 2
= [10 + 12 + 10] / 2
= 16cm
Area of △ABC = √s (s – a) (s – b) (s – c)
= √(16) (16 – 10) (16 – 12) (16 – 10)
= √16 * 6 * 4 * 6
= 48cm2
[c] Area of △ABC = area of △AOB + area of △BOC + area of △COA48 = (1 / 2) * 10 * r + (1 / 2) * 12 * r + (1 / 2) * 10 * r
48 * 2 = r (10 + 12 + 10)
48 * 2 = 32 * r
r = 3cm
Question 24:

From a tin sheet, a sector of radius 20cm and central angle 240o is divided into 4 equal parts as shown in the figure. The shaded portion is cut off. Using this, a vessel in the shape of a square pyramid is made. What is the capacity of this vessel?
Solution:

In ΔOBC,
∠O = ∠B = ∠C = 600
OB = BC = OC = 20 cm
e = 20 cm
a = 20 cm => d = 20√2
h2 = e2 – (d / 2)2 = 202 – (10√2)2
= 400 – 200
= 200
h = √200 = 10√2 cm
Volume = [1 / 3] a2h
= [1 / 3] x 202 x 10√2
= 4000√2 / 3 cm3
Question 25:

In the figure, the radius of the smaller circle is 3cm, that of the bigger circle is 6cm and the distance between the centres of the circles is 15cm. PQ is a tangent to both circles. Find its length.
Solution:

In ΔAPC and ΔBQC
∠P = ∠Q = 900
∠ACP = ∠BCQ
ΔAPC ~ ΔBQC
AP / AC = BQ / BC
3 / x = 6 / 15 – x
6x = 3(15 – x)
= 45 – 3x
9x = 45
x = 5
AP = 3 cm, AC = 5 cm
=> PC = 4 cm
BQ = 6 cm, BC = 10 cm
=> QC = 8 cm
PQ = PC + QC
= 4 + 8
PQ = 12 cm

Comments