In Geometry, one of the special kind of angles is alternate angles. Alternate angles are the set of non-adjacent angles on either side of the transversal. In this article, let us discuss the proper definition of alternate angle, types, theorem, and an example in detail.
Table of Contents:
Alternate Angle Definition
If a straight line intersects two or more parallel lines, then it is called a transversal line. When the coplanar lines are cut by a transversal, some angles are formed. Those angles are known as interior or exterior angles. Alternate angles are shaped by the two parallel lines crossed by a transversal.

Consider the given figure,
EF and GH are the two parallel lines.
RS is the transversal line that cuts EF at L and GH at M
If two parallel lines are cut by a transversal, then the alternate angles are equal.
Therefore, ∠3 = ∠ 5 and ∠4 = ∠6
Types of Alternate Angles
Based on the position of the angles, the alternate angles are classified into two types, namely
- Alternate Interior Angles – Alternate interior angles are the pair of angles on the inner side of the two parallel lines but on the opposite side of the transversal.
From the above-given figure,
∠3, ∠4, ∠5, ∠6 are the alternate interior angles
- Alternate Exterior Angles – Alternate exterior angles are the pair of angles on the outer side of the two parallel lines but on the opposite side of the transversal.
From the above-given figure,
∠1, ∠2, ∠7, ∠8 are the alternate exterior angles
Alternate Angles Theorem
Alternate angle theorem states that when two parallel lines are cut by a transversal, then the resulting alternate interior angles or alternate exterior angles are congruent.
To prove:
If two parallel lines are cut by a transversal, then the alternate interior angles are equal.
Proof:
Assume that PQ and RS are the two parallel lines cut by a transversal LM. W, X, Y, Z are the angles created by a transversal
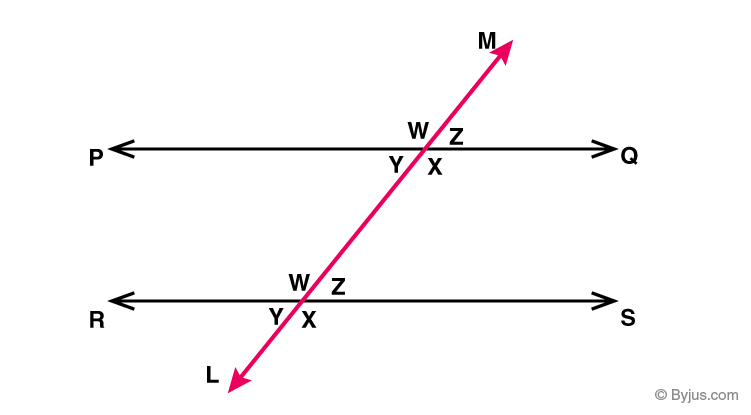
At the intersection point on the straight lines PQ and LM,
∠W + ∠Z = 180° (PQ is the straight line)—-(1)
∠X + ∠Z = 180° (LM is the straight line)—-(2)
So, from (1) and (2), we get
∠W = ∠X
Again, at the intersection point on the straight lines RS and LM,
∠W + ∠Z = 180° (RS is the straight line)—-(3)
∠W + ∠Y = 180° (LM is the straight line)—-(4)
So, from (3) and (4), we get
∠Z = ∠Y
Therefore, it is concluded that the alternate interior angles are congruent.
Hence, proved.
Video Lesson on Types of Angles

Alternate Angles Example
Question:
From the given figure, find the angles Y, X, and Z.

Solution:
Given:
∠Y = 60°
From the alternate interior angle theorem, ∠Y = ∠Z.
Therefore, the value must be equal.
∠Z = 60°
Since RS is the straight line, ∠W + ∠Z = 180°
So, ∠W = 180° – ∠Z
Substitute the value ∠Z = 60°
∠W = 180° – 60°
∠W = 120°
Again, from the alternate interior angle theorem, ∠W = ∠X.
Therefore, ∠X = 120°
Visit BYJU’S – The Learning App for Maths- related concepts, theorems, proofs, examples and also watch engaging videos.
| Related Links | |
| Lines and Angles | Corresponding Angles |
| Supplementary Angles | Vertical Angles |
Frequently Asked Questions on Alternate Angles
What is meant by alternate angles?
The alternate angles are the pair of angles, which are formed when the coplanar lines are cut by a transversal.
What are the two different types of alternate angles?
The two different types of alternate angles are:
Alternate interior angles
Alternate exterior angles
What is called alternate interior angles?
Alternate interior angles are the pair of angles that are formed on the inner side of the two parallel lines but on the opposite side of the transversal.
What is called the alternate exterior angle?
Alternate exterior angles are the pair of angles that are formed on th outer side of the parallel lines but on the opposite side of the transversal.
Is alternate interior angles are congruent or supplementary?
Yes, the alternate interior angles are congruent, whereas the consecutive interior angles are supplementary.
