Supplementary angles are those angles that sum up to 180 degrees. For example, angle 130° and angle 50° are supplementary angles because sum of 130° and 50° is equal to 180°. Similarly, complementary angles add up to 90 degrees. The two supplementary angles, if joined together, form a straight line and a straight angle.
But it should be noted that the two angles that are supplementary to each other, do not have to be next to each other. Hence, any two angles can be supplementary angles, if their sum is equal to 180°.
Geometry is one of the important branches of mathematics that deals with the study of different shapes. It initiates the study of lines and angles. A straight line is a line without curves and it is defined as the shortest distance between two points. An angle is formed when the line segment meets at a point.
| Table of contents: |
What are Supplementary Angles?
In Maths, the meaning of supplementary is related to angles that make a straight angle together. It means, two angles are said to be supplementary angles when they add up to 180 degrees. Two angles are supplementary, if
- One of its angles is an acute angle and another angle is an obtuse angle.
- Both of the angles are right angles.
This means that ∠A + ∠B = 180°.
See the figure below for a better understanding of the pair of angles that are supplementary.
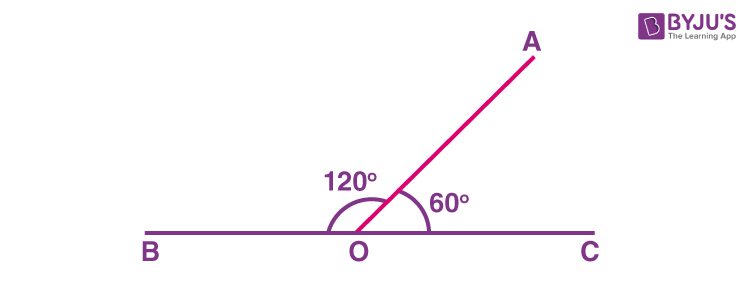
Examples of Supplementary Angles
Some of the examples of supplementary angles are:
- 120° + 60° = 180°
- 90° + 90° = 180°
- 140° + 40° = 180°
- 96° + 84° = 180°
Properties of Supplementary Angles
The important properties of supplementary angles are:
- The two angles are said to be supplementary angles when they add up to 180°.
- The two angles together make a straight line, but the angles need not be together.
- “S” of supplementary angles stands for the “Straight” line. This means they form 180°.
Adjacent and Non-Adjacent Supplementary Angles
There are two types of supplementary angles:
- Adjacent supplementary angles
- Non-adjacent supplementary angles
Adjacent Supplementary angles
The supplementary angles that have a common arm and a common vertex are called adjacent supplementary angles. The adjacent supplementary angles share the common line segment and vertex with each other.
For example, the supplementary angles 110° and 70°, in the given figure, are adjacent to each other.

Non-adjacent Supplementary angles
The supplementary angles that do not have a common arm and a common vertex are called non-adjacent supplementary angles. The non-adjacent supplementary angles do not share the line segment or vertex with each other.
For example, the supplementary angles 130° and 50°, in the given figure, are non-adjacent to each other.

How to Find Supplementary Angles?
As we know, if the sum of two angles is equal to 180°, then they are supplementary angles. Each of the angles is said to be a supplement of another angle. Hence, we can determine the supplement of an angle, by subtracting it from 180°.
For example, if you had given that two angles that form supplementary angles. If one angle is ∠A then another angle ∠B is its supplement. Hence,
∠A = 180° – ∠B (or)
Supplementary Angles Theorem
The supplementary angle theorem states that if two angles are supplementary to the same angle, then the two angles are said to be congruent.
Proof:
If ∠x and ∠y are two different angles that are supplementary to a third angle ∠z, such that,
∠x + ∠z = 180 ……. (1)
∠y + ∠z = 180 ……. (2)
Then, from the above two equations, we can say,
∠x = ∠y
Hence proved.
Supplementary and Complementary Angles
Both supplementary and complementary angles are pairs of angles, that sum up to 180° and 90°, respectively. Let us find more differences between the pair of angles.
| Complementary Angles | Supplementary Angles |
| Sum of two angles is 90° | Sum of two angles is 180° |
| Ex: ∠A + ∠B = 90°. | Ex: ∠A + ∠B = 180°. |
| Complementary angles form a right-angled triangle when combined together. | Supplementary angles form a straight line. |
| The complement of an angle A is (90 – A)° | The supplement of an angle A is (180 – A)° |
Video Lesson on Types of Angles

Related Articles
- Straight Angle
- Corresponding Angles
- Linear pairs of angles
- Alternate angles
- Vertically opposite angles
Problems and Solutions on Supplementary angles
Question 1: Find the measure of an unknown angle from the given figure.

Solution:
We know that the supplementary angles add up to 180°.
X + 55° + 40° = 180°
X + 95° = 180°
X = 180°- 95°
X = 85°
Therefore, the unknown angle, X = 85°
Question 2: If ∠x and ∠y are supplementary angles and ∠x = 67, then find ∠y.
Solution: Given, ∠x and ∠y are supplementary angles
And
∠x = 67°
Since, ∠x + ∠y = 180°
∠y = 180 – ∠x
∠y = 180 – 67
∠y = 113°
Question 3: The two given angles are supplementary. If the estimate of the angle is two times the estimate of the other, what is the measure of each angle?
Answer:
Assume the measure of one of the angles that are supplementary to be “a”.
The estimate of the angle is two times the estimate of the other.
The measure of the other angle is 2a.
If the total of the estimates of the given two angles is 180°, then the angles are termed supplementary.
The 2 supplementary angles are 60 and 120.
Question 4: The two angles P and Q are supplementary, find the angles given that
∠P = 2x + 15 and ∠Q = 5x – 38.
Answer:
If the total of the estimates of the given two angles is 180°, then the angles are termed supplementary.
∠P + ∠Q = 180
It is given that ∠P = 2x + 15 and ∠Q = 5x – 38.
Substitute the values of P and Q respectively.
Question 5: What are the values of angles A and B if the value of angles A and B are supplementary in a way that angle A = 2x + 10 and angle B = 6x – 46?
Answer:
If the total of the estimates of the given two angles is 180°, then the angles are termed supplementary.
∠A + ∠B = 180
(2x + 10) + (6x – 46) = 180
8x – 36 =180
8x = 216
x = 216 / 8
x = 27
A = 2x + 10 and angle B = 6x – 46
Angle A = 2 (27) + 10 = 64
Angle B = 6 (27) – 46 = 116
Question 6: The given two angles are supplementary in nature. The estimates of the bigger angle are five times greater than four times the estimate of the lesser angle. Find the measure of the larger angle.
Answer:
If the total of the estimates of the given two angles is 180°, then the angles are termed supplementary.
Assume the two angles supplementary angles to be x (bigger angle) and y (smaller angle).
According to the question,
x = 4y + 5
x + y =180
(4y + 5) + y =180
5y + 5 =180
5y = 175 = 35
The bigger angle = x = 4 * (35) + 5 = 145
Question 7: The two supplementary angles are in the ratio three : two. What are the angles?
Answer:
Assume the two supplementary angles to be 3x and 2x.
If the total of the estimates of the given two angles is 180°, then the angles are termed supplementary.
3x + 2x = 180
5x = 180
x = 180 / 5 = 36
x = 36
The angle are 3x = 3 * 36 = 108 and
2x = 2 * 36 = 72
Therefore, the two supplementary angles are 108 and 72.
Practice Questions
- What is the supplement of angle 65 degrees?
- Are the angles 80° and 120° supplementary?
- Find the supplement of 140°.
Stay tuned with BYJU’S – The Learning App to learn the mathematical concepts and also watch engaging videos to learn with ease.
Frequently Asked Questions – FAQs
Can 2 Acute Angles be Supplementary Angles?
By definition, acute angles are the angles that measure the angle greater than 0° and less than 90°. If you add two acute angles in which each angle is large as possible, its sum will be less than 180°. By the definition of supplementary angles, it is impossible to get the supplementary angle when we add two acute angles.
Example: 80° +60° = 140° which is not a supplementary angle.
But, in this case, if we add more than two acute angles, we can get supplementary angles.
Can 2 Obtuse Angles be Supplementary Angles?
By the definition of obtuse angles, the angles that measure greater than 90° are obtuse. If you add two obtuse angles, the sum will be greater than 180°. It will not satisfy the property of the supplementary angles when we add obtuse angles.
Example: 110° + 95° = 205° which is not a supplementary angle. [205° > 180° ]
Can 2 Right Angles be Supplementary Angles?
When two right angles are added, it is possible to get the supplementary angle. because 90° + 90° = 180°, as it satisfies the condition of supplementary angles.

