Linear pair of angles are formed when two lines intersect each other at a single point. The angles are said to be linear if they are adjacent to each other after the intersection of the two lines. The sum of angles of a linear pair is always equal to 180°. Such angles are also known as supplementary angles. The adjacent angles are the angles which have a common vertex. Hence, here as well the linear angles have a common vertex. Also, there will be a common arm which represents both the angles. A real-life example of a linear pair is a ladder which is placed against a wall, forms linear angles at the ground.
Linearity represents one which is straight. So here also, linear angles are the one which is formed into a straight line. The pair of adjacent angles here are constructed on a line segment, but not all adjacent angles are linear. Hence, we can also say, that linear pair of angles is the adjacent angles whose non-common arms are basically opposite rays.
Explanation for Linear Pair of Angles
When the angle between the two lines is 180°, they form a straight angle. A straight angle is just another way to represent a straight line. A straight line can be visualized as a circle with an infinite radius. A line segment is any portion of a line which has two endpoints. Also, a portion of any line with only one endpoint is called a ray.
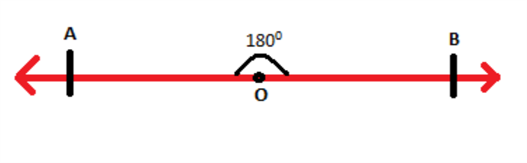
The figure shown below represents a line segment AB and the two arrows at the end indicate a line.

If a point O is taken anywhere on the line segment AB as shown, then the angle between the two line segments AO and OB is a straight angle i.e. 180°.
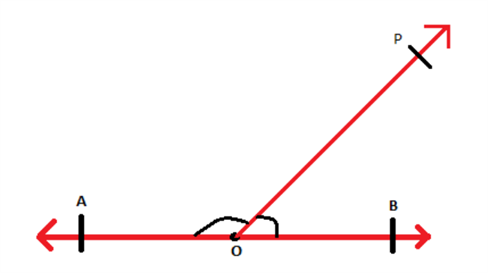
The angles which are formed at O are ∠POB and ∠POA. It is known that the angle between the two line segments AO and OB is 180°. therefore, the angles ∠POB and ∠POA add up to 180°.
Thus, ∠POB + ∠POA = ∠AOB = 180°
∠POB and ∠POA are adjacent to each other and when the sum of adjacent angles is 180° then such angles form linear pair of angles.
The above discussion can be stated as an axiom.
Also, read:
Axioms
Axiom 1: If a ray stands on a line then the adjacent angles form a linear pair of angles.

In the figure above, all the line segments pass through the point O as shown. As the ray OA lies on the line segment CD, angles ∠AOD and ∠AOC form a linear pair. Similarly, ∠QOD and ∠POD form a linear pair and so on.
The converse of the stated axiom is also true, which can also be stated as the following axiom.
Axiom 2: If two angles form a linear pair, then uncommon arms of both the angles form a straight line.

In the figure shown above, only the last one represents a linear pair, as the sum of the adjacent angles is 180°. Therefore, AB represents a line. The other two pairs of angles are adjacent but they do not form a linear pair. They do not form a straight line.
The two axioms mentioned above form the Linear Pair Axioms and are very helpful in solving various mathematical problems.
Video Lesson on Types of Angles

Example
Suppose two angles ∠AOC and ∠ BOC form a linear pair at point O in a line segment AB. If the difference between the two angles is 60°. Then find both the angles.
Solution: Given, ∠AOC and ∠ BOC form a linear pair
So, ∠AOC + ∠ BOC =180° ………(1)
Also given,
∠AOC – ∠ BOC = 60° ………(2)
Adding eq. 1 and 2, we get;
2∠AOC = 180° + 60° = 240°
∠AOC = 240°/2 = 120°
Now putting the value of ∠AOC in equation 1, we get;
∠BOC = 180° – ∠AOC = 180° – 120°
∠BOC = 60°
There is a lot more to learn about lines and angles. To know more about properties of pair of angles, download BYJU’S – The Learning App from Google Play Store.


Comments