Adjacent angles and vertical angles are two different types of pairs of angles. These angles are the major concept of geometry, introduced to us in Class 4 and 5. The angles are the basic concept that is studied throughout academics. There are various types of angles we learn at school.
The measure of rotation of a ray, when it is rotated about its endpoint is known as the angle, formed by the ray between its initial and final position. An angle is formed by two rays, that are connected end-to-end.
At times, in geometry, a pair of angles are used. There are various kinds of pairs of angles, like – supplementary angles, complementary angles, adjacent angles, linear pair of angles, opposite angles, etc. In this article, we are going to discuss the definition of adjacent angles and vertical angles in detail.
What are Adjacent Angles?
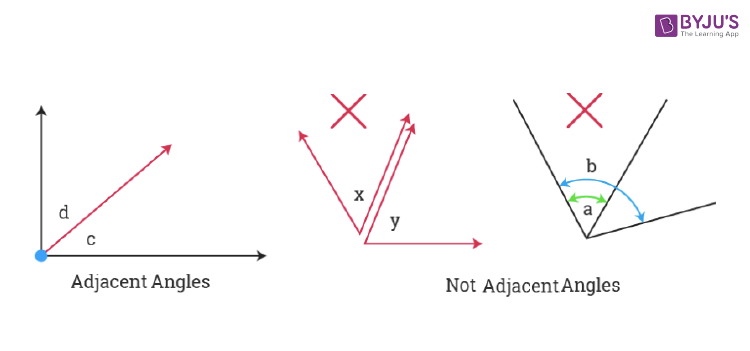
The two angles are said to be adjacent angles when they share the common vertex and side. The endpoint of the rays, forming the sides of an angle, is called the vertex of an angle. Adjacent angles can be a complementary angle or supplementary angle when they share the common vertex and side.
- If the sum of adjacent angles is equal to 90 degrees, then they are complementary to each other
- If the sum of adjacent angles is equal to 180 degrees, then they are supplementary to each other
Adjacent Angle Examples
Consider a wall clock, The minute hand and second hand of the clock form one angle represented as ∠AOC and the hour hand forms another angle with the second hand represented as∠COB. Both these pairs of angles i.e.∠AOC and ∠COB lie next to each other and are known as adjacent angles.

∠AOC and ∠COB have a common vertex, a common arm and the uncommon arms lie on either side of the common arms. Such angles are known as adjacent angles.
Properties of Adjacent Angles
Some of the important properties of the adjacent angles are as follows:
Two angles are adjacent-angles, such that
- They share the common vertex
- They share the common arm
- Adjacent angles do not overlap each other
- It does not have a common interior-point
- Adjacent angles can be complementary or supplementary angles when they share the common vertex.
- There should be a non-common arm on both sides of the common arm
Adjacent Supplementary Angles
What is the sum of adjacent angles? The adjacent angles will have the common side and the common vertex. Two angles are said to be supplementary angles if the sum of both the angles is 180 degrees. If the two supplementary angles are adjacent to each other then they are called linear pair.
Sum of two adjacent supplementary angles = 180o.
Here are some examples of Adjacent angles:

Adjacent angles – Linear Pair
Pair of adjacent angles whose measures add up to form a straight angle is known as a linear pair. The angles in a linear pair are supplementary.

The angles ∠POB and ∠POA are formed at O. ∠POB and ∠POA are adjacent angles and they are supplementary i.e. ∠POB + ∠POA = ∠AOB = 180°
∠POB and ∠POA are adjacent to each other and when the sum of adjacent angles is 180° then such angles form a linear pair of angles.
What are Vertical Angles?
When a pair of lines intersect, as shown in the fig. below, four angles are formed. ∠AOD and ∠COB are vertically opposite to each other and ∠AOC and ∠BOD are vertically opposite to each other. These angles are also known as vertical angles or vertically opposite angles.

Thus, when two lines intersect, two pairs of vertically opposite angles are formed i.e. ∠AOD, ∠COB and ∠AOC, ∠BOD.
According to the vertical angle theorem, in a pair of intersecting lines, the vertically opposite angles are equal.
Difference Between Adjacent and Vertical Angles
| Adjacent angles | Vertical angles |
| Two angles with a common arm and vertex are called adjacent angles | When two lines intersect each other, then the pair of opposite angles formed at the vertex are called vertical angles |
| They share a common arm and common vertex | They share a common vertex, but no common arm |
| Adjacent angles are not always equal in measure | Vertically opposite angles are equal in measure |
Solved Examples
Example 1: Find the value of x.

If m∠AOB = 110° , m∠COB = x and m∠AOC= 70°
Solution:
From figure:
m∠AOB = 110°
m∠AOC = 70°
m∠ COB = x
Now, from figure: ∠AOB = ∠AOC + ∠COB
m∠AOB = m∠AOC + m∠COB
110° = 70° + x
x = 110° – 70°
x = 30°
Example 2: In the given figure, is ∠1 adjacent to ∠2? Give an answer with justification.

Solution:
In the given figure, ∠1 does not share the vertex of ∠2.
As it does not obey the important property of adjacent angles, therefore,
∠1 is not adjacent to ∠2.
Related Articles
To learn more about angles and other concepts download BYJU’S-The Learning App. Happy Learning!!!
Frequently Asked Questions on Adjacent and Vertical angles
What are Adjacent Angles?
Adjacent angles can be defined as two angles that have a common vertex and a common side. Two adjacent angles can be either complementary or supplementary based on their sum value.
What are Vertical Angles?
Vertical angles are defined as the angles opposite to each other when two lines cross (i.e. intersect). It is also known as vertically opposite angles. It should be noted that two vertical angles are always equal.
Can Vertical Angles be Adjacent?
No, vertical angles can never be adjacent. Adjacent angles are the ones next to each other while vertical angles are opposite from each other.


Comments