Area of a square is defined as the number of square units needed to fill a square. In general, the area is defined as the region occupied inside the boundary of a flat object or 2d figure. The measurement is done in square units, with the standard unit being square metres (m2).
For the computation of area, there are pre-defined formulas for squares, rectangles, circles, triangles, etc. In this article, you will learn about the area of a square.
| Table of Contents: |
What is Area?
The area is the space covered by the object. It is the region occupied by any shape. While measuring the area of a square, we consider only the length of its side. All sides of a square are equal; hence, its area is equal to the square of the side.
Similarly, we can find the area of the other shapes such as rectangles, parallelograms, triangles or any polygon, based on its sides. The area of the surface is calculated based on the radius or the distance of its outer line from the axis for curved surface objects.
Example: circle
Learn more: What is mathematics?
Area of a Square Formula
Before moving into the area of square formula used for calculating the region occupied, let us try using graph paper. You are required to find the area of a side 5 cm. Using this dimension, draw a square on a graph paper having 1 cm × 1 cm squares. The square covers 25 complete squares.
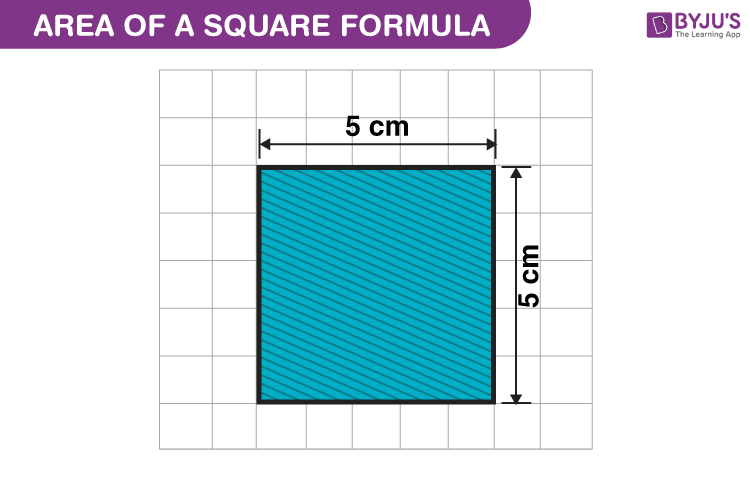
Thus, the area of the square is 25 square cm, which can be written as 5 cm × 5 cm, that is, side × side.
From the above discussion, it can be inferred that the formula can give the area of a square is:
Area of a Square = Side × Side
Therefore, the area of square = Side2 square units
and the perimeter of a square = 4 × side units
Here some of the unit conversion lists are provided for reference. Some conversions of units:
- 1 m = 100 cm
- 1 sq. m = 10,000 sq. cm
- 1 km = 1000 m
- 1 sq. km = 1,000,000 sq. m
Area of a Square Sample Problems
Example 1:
Find the area of a square clipboard whose side measures 120 cm.
Solution:
Side of the clipboard = 120 cm = 1.2 m
Area of the clipboard = side × side
= 120 cm × 120 cm
= 14400 sq. cm
= 1.44 sq. m
Example 2:
The side of a square wall is 75 m. What is the cost of painting it at the rate of Rs. 3 per sq. m?
Solution:
Side of the wall = 75 m
Area of the wall = side × side = 75 m × 75 m = 5,625 sq. m
For 1 sq. m, the cost of painting = Rs. 3
Thus, for 5,625 sq. m, the cost of painting = Rs. 3 × 5,625 = Rs 16,875
Example 3:
A courtyard’s floor which is 50 m long and 40 m wide is to be covered by square tiles. The side of each tile is 2 m. Find the number of tiles required to cover the floor.
Solution:
Length of the floor = 50 m
The breadth of the floor = 40 m
Area of the floor = length × breadth = 50 m × 40 m = 2000 sq. m
Side of one tile = 2 m
Area of one tile = side ×side = 2 m × 2 m = 4 sq. m
No. of tiles required = area of floor/area of a tile = 2000/4 = 500 tiles.
Practice Problems
- A square wall of length 25 metres, has to be painted. If the cost of painting per square metre is ₹ 4.50. Find the cost of painting the whole wall.
- Find the length of a square park whose area is 3600 square metres.
- Find the area of the square whose length of the diagonal is 5√2 cm.
To learn and practice more problems related to the area of a square, download BYJU’S-The Learning App.
| Related Links | |
| Area of a Circle | Area of a Triangle |
| Area of a Rectangle | Area of a Rhombus |
Frequently Asked Questions on Area of Square
What is the area of a square?
As we know, a square is a two-dimensional figure with four sides. It is also known as a quadrilateral. The area of a square is defined as the total number of unit squares in the shape of a square. In other words, it is defined as the space occupied by the square.
Why is the area of a square a side square?
A square is a 2D figure in which all the sides are of equal measure. Since all the sides are equal, the area would be length times width, which is equal to side × side. Hence, the area of a square is side square.
What is the area of a square formula?
The area of a square can be calculated using the formula side × side square units.
How to find the area of a square if a diagonal is given?
If the diagonal of a square is given, then the formula to calculate the area of a square is:
A = (½) × d2 square units.
Where “d” is the diagonal
What is the perimeter and the area of a square?
The perimeter of the square is the sum of all the four sides of a square, whereas the area of a square is defined as the region or the space occupied by a square in the two-dimensional space.
What is the area of a square if its side length is 10 cm?
Given: Side = 10 cm
We know that, Area of a square = Side × Side square units
Thus, Area = 10 × 10 = 100 cm2
Therefore, the area of a square is 100 cm2 if its side length is 10 cm.
What is the unit for an area of square?
The area of a square is measured in square units.
How to calculate the area of a square if its perimeter is given?
Follow the below steps to find the area of a square if its perimeter is given:
Step 1: Find the side length of a square using the perimeter formula, P = 4 × Side
Step 2: Substitute the side length in the area formula: A = Side × Side.

this web site very better
I need formulas of rectangle
Please visit: https://byjus.com/rectangle-formula/
Length × width
Find the length of a side of square cardboard whose perimeter is hundred CM and find the area
Perimeter of square = 100 cm
4 x side = 100
Length of side = 100/4 = 25 cm
Now,
area of square = side^2 = 25^2 = 625 sq.cm.