In this lesson, the steps for constructing a square are explained with diagrams. To recall, a square is a quadrilateral and a polygon that has 4 vertices and 4 sides enclosing 4 angles. The sum of its interior angles is 360°. A quadrilateral, in general, has sides of different lengths and angles of different measures. However, squares, rectangles, etc. are special types of quadrilaterals with some of their sides and angles being equal. In this article, we will discuss the construction of this special quadrilateral, that is, the construction of squares.
Steps for Construction of Square
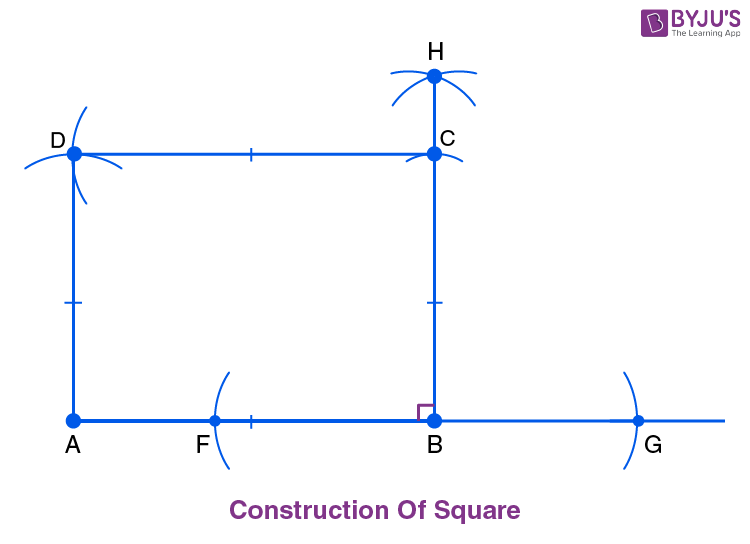
As mentioned, a square is a quadrilateral with sides of equal length and angles of the same measure. Let us say you are required to construct a square. The only dimension provided is the length of one of its sides, 5 cm. We know that the 4 interior angles of the square measure 90 degrees each. Hence, we do not require any other dimension for the construction of a square. All the sides are equal in measurement and are perpendicular.
The steps for square construction are as follows:
- Step 1: Draw a line segment AB of 5 cm.

- Step 2: Extend the line AB and using a compass, mark two arcs from B on the line. Mark the points as F and G.

- Step 3: Mark arcs from points F and G above the line. The point where the arcs meet is named H.
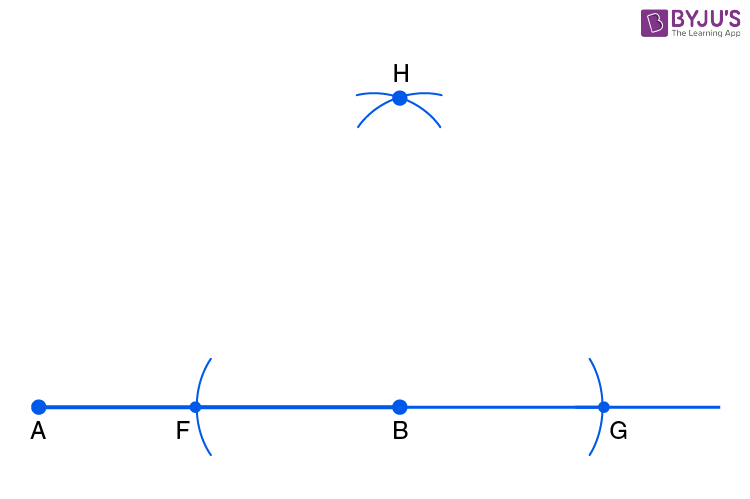
- Step 4: Join points B and H.
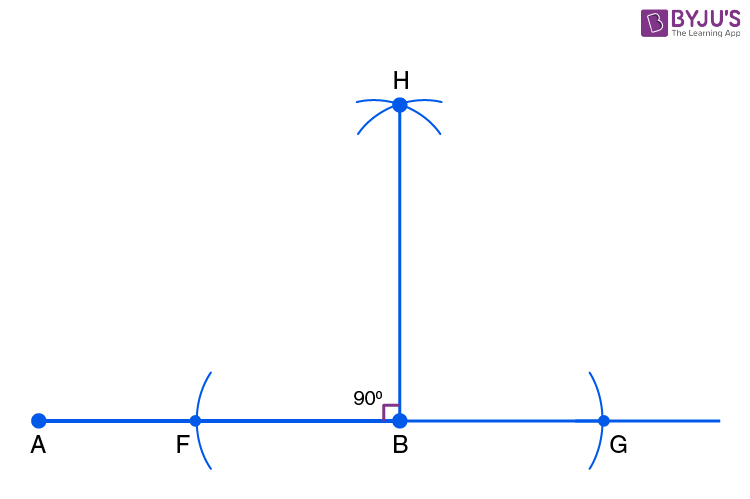
- Step 5: Set the compass to a radius of 5 cm and mark the arc from points A and B. The point where the arc intersects BH is the vertex C of the square.
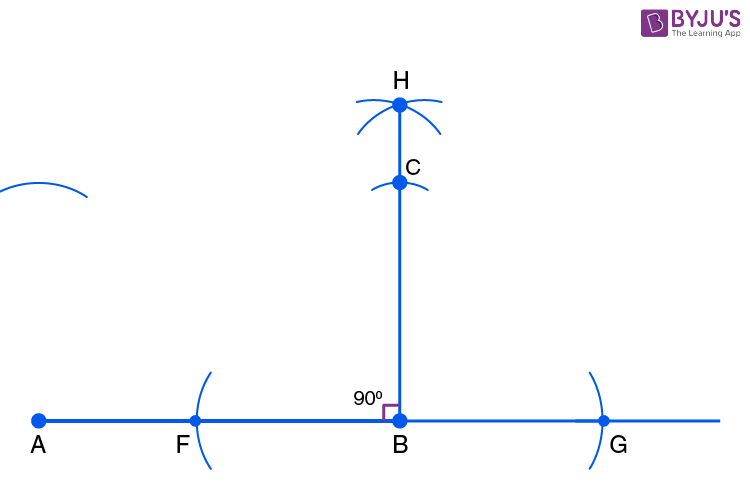
- Step 6: With the same radius of 5 cm on the compass, mark an arc from the point C on the previously drawn arc above the point A. Mark their point of intersection as D.
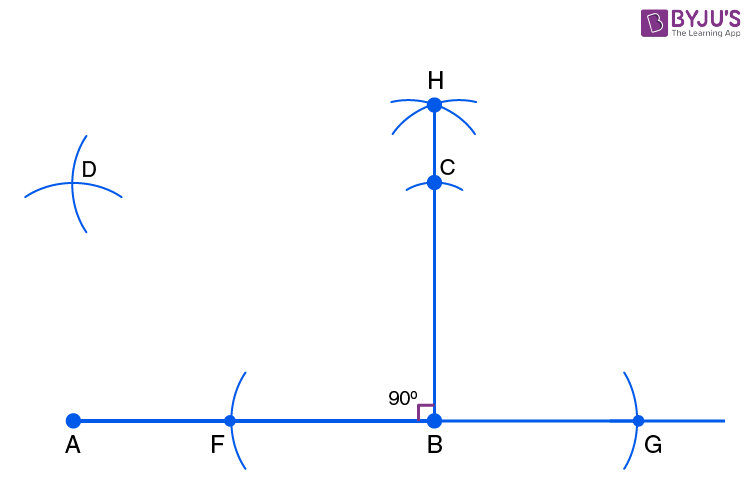
- Step 7: Join the points C and D as well as A and D to get the required square ABCD.
This was all about the square construction. Using these steps, the square of any dimensions can be constructed easily.
Access NCERT Solutions for Class 9 Maths Chapter 11 Constructions here.
More Construction Related Articles
| Construction Of Angles | Construction Of Quadrilaterals |
| Triangle Construction | Construction Of Parallel Lines |
| Construction Of Similar Triangles | Constructions Class 9 |

Comments