The greatest integer function is a function that results in the integer nearer to the given real number. It is also called the step function. The greatest integer function rounds off the given number to the nearest integer. Hence, the formula to find the greatest integer is very simple. It is represented by the symbol ⌊x⌋, where x is any value.
What is the Greatest Integer Function?
The greatest integer function is denoted by ⌊x⌋, for any real function. The function rounds – off the real number down to the integer less than the number. This function is also known as the Floor Function.
For example:
- ⌊1.15⌋ = 1
- ⌊4.56567⌋ = 4
- ⌊50⌋ = 50
- ⌊-3.010⌋ = -4
| Read more: |
Greatest integer function domain and range
The domain of the greatest integer function is a group of real numbers that are divided into intervals like [-4, 3), [-3, 2), [-2, 1), [-1, 0) and so on. Its range will be the integers that are evaluated.
| Values of x (Domain) | ⌊x⌋ (Range) |
| 2.2 | ⌊2.2⌋ = 2 |
| 3.99 | ⌊3.99⌋ = 3 |
| 9 | ⌊9⌋ = 9 |
Greatest Integer Function Properties
The important properties of greatest integer function are:
- ⌊x⌋ = x, where x is an integer
- ⌊x + n⌋ = ⌊x⌋ + n, where n ∈ Z
- ⌊-x] = –⌊x], if x ∈ Z
- ⌊-x] =-⌊x] – 1, if x ∉ Z
- If ⌊f(x)] ≥ Y, then f(x) ≥ Y
Note: Z stands for set of integers.
Video Lessons
Greatest Integer Function

Greatest Integer Function-Applied

Greatest integer function graph
When the intervals are in the form of (n, n+1), the value of greatest integer function is n, where n is an integer.
For example, the greatest integer function of the interval [3,4) will be 3.
The graph is not continuous. For instance, below is the graph of the function f(x) = ⌊ x ⌋.
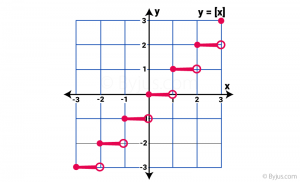
The above graph is viewed as a group of steps and hence the integer function is also called a Step function. The left endpoint in every step is blocked(dark dot) to show that the point is a member of the graph, and the other right endpoint (open circle) indicates the points that are not part of the graph.
You can observe that in every interval, the function f(x) is the same. The function’s value stays constant within an interval. For instance, the value of function f(x) is equal to -5 in the interval [-5, -4).
Solved Examples on Greatest Integer Function
Let’s Workout:
Example 1: Find the greatest integer function for following
(a) ⌊-261⌋
(b) ⌊3.501⌋
(c) ⌊-1.898⌋
Solution:
According to the greatest integer function definition
(a) ⌊-261⌋ = -261
(b) ⌊3.501⌋ = 3
(c) ⌊-1.898⌋ = -2
Example 2: Evaluate ⌊3.7⌋.
Solution:
On a number line, ⌊3.7⌋ lies between 3 and 4
The largest integer which is less than 3.7 is 3.
So, ⌊3.7⌋ = 3 Answer!
To know more about the greatest integer function and least integer function, you can register with BYJU’S and get access to various interactive videos to make your learning easy and interesting.
Comments