In Mathematics, integers are the collection of whole numbers and negative numbers. Similar to whole numbers, integers also does not include the fractional part. Thus, we can say, integers are numbers that can be positive, negative or zero, but cannot be a fraction. We can perform all the arithmetic operations, like addition, subtraction, multiplication and division, on integers. The examples of integers are, 1, 2, 5,8, -9, -12, etc. The symbol of integers is “Z“. Now, let us discuss the definition of integers, symbol, types, operations on integers, rules and properties associated to integers, how to represent integers on number line with many solved examples in detail.

| Table of contents: |
What are Integers?
The word integer originated from the Latin word “Integer” which means whole or intact. Integers is a special set of numbers comprising zero, positive numbers and negative numbers.
Examples of Integers: – 1, -12, 6, 15.
Symbol
The integers are represented by the symbol ‘Z’.
Z= {……-8,-7,-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8,……}
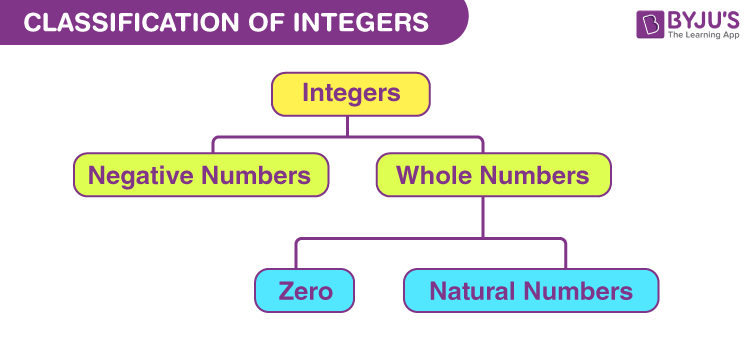
Types of Integers
Integers come in three types:
- Zero (0)
- Positive Integers (Natural numbers)
- Negative Integers (Additive inverse of Natural Numbers)
Zero
Zero is neither a positive nor a negative integer. It is a neutral number i.e. zero has no sign (+ or -).
Positive Integers
The positive integers are the natural numbers or also called counting numbers. These integers are also sometimes denoted by Z+. The positive integers lie on the right side of 0 on a number line.
| Z+ → 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30,…. |
Negative Integers
The negative integers are the negative of natural numbers. They are denoted by Z–. The negative integers lie on the left side of 0 on a number line.
| Z– → -1, -2, -3, -4, -5, -6, -7, -8, -9, -10, -11, -12, -13, -14, -15, -16, -17, -18, -19, -20, -21, -22, -23, -24, -25, -26, -27, -28, -29, -30,….. |
How to Represent Integers on Number Line?
As we have already discussed the three categories of integers, we can easily represent them on a number line based on positive integers, negative integers and zero.
Zero is the centre of integers on a number line. Positive integers lie on the right side of zero and negative integers lie on the left. See the below figure.
Rules of Integers
Rules defined for integers are:
- Sum of two positive integers is an integer
- Sum of two negative integers is an integer
- Product of two positive integers is an integer
- Product of two negative integers is an integer
- Sum of an integer and its inverse is equal to zero
- Product of an integer and its reciprocal is equal to 1
Arithmetic Operations on Integers
The basic Maths operations performed on integers are:
- Addition of integers
- Subtraction of integers
- Multiplication of integers
- Division of integers
Addition of Integers
While adding the two integers with the same sign, add the absolute values, and write down the sum with the sign provided with the numbers.
For example,
(+4) + (+7) = +11
(-6) + (-4) = -10
While adding two integers with different signs, subtract the absolute values, and write down the difference with the sign of the number which has the largest absolute value.
For example,
(-4) + (+2) = -2
(+6) + (-4) = +2.
Subtraction of Integers
While subtracting two integers, change the sign of the second number which is being subtracted, and follow the rules of addition.
For example,
(-7) – (+4) = (-7) + (-4) = -11
(+8) – (+3) = (+8) + (-3) = +5
Multiplication of Integers
While multiplying two integer numbers, the rule is simple.
- If both the integers have the same sign, then the result is positive.
- If the integers have different signs, then the result is negative.
For example,
- (+2) x (+3) = +6
- (+3) x (-4) = – 12
Thus, we can summarise the multiplication of two integers with examples in the below table.
| Multiplication of Signs | Resulting Sign | Examples |
| + × + | + | 3 × 4 = 12 |
| + × – | – | 3 × -4 = -12 |
| – × + | – | -3 × 4 = -12 |
| – × – | + | -3 × -4 = 12 |
Division of Integers
The rule for dividing integers is similar to multiplication.
- If both the integers have the same sign, then the result is positive.
- If the integers have different signs, then the result is negative.
Similarly
- (+6) ÷ (+2) = +3
- (-16) ÷ (+4) = -4
| Division of Signs | Resulting sign | Examples |
| + ÷ + | + | 15 ÷ 3 = 5 |
| + ÷ – | – | 15 ÷ -3 = -5 |
| – ÷ + | – | -15 ÷ 3 = -5 |
| – ÷ – | + | -15 ÷ -3 = 5 |
Properties of Integers
The major Properties of Integers are:
- Closure Property
- Associative Property
- Commutative Property
- Distributive Property
- Additive Inverse Property
- Multiplicative Inverse Property
- Identity Property
Closure Property
According to the closure property of integers, when two integers are added or multiplied together, it results in an integer only. If a and b are integers, then:
- a + b = integer
- a x b = integer
Examples:
- 2 + 5 = 7 (is an integer)
- 2 x 5 = 10 (is an integer)
Commutative Property
According to the commutative property of integers, if a and b are two integers, then:
- a + b = b + a
- a x b = b x a
Examples:
- 3 + 8 = 8 + 3 = 11
- 3 x 8 = 8 x 3 = 24
But for the commutative property is not applicable to subtraction and division of integers.
Associative Property
As per the associative property , if a, b and c are integers, then:
- a+(b+c) = (a+b)+c
- ax(bxc) = (axb)xc
Examples:
- 2+(3+4) = (2+3)+4 = 9
- 2x(3×4) = (2×3)x4 = 24
Similar to commutativity, associativity is applicable for the addition and multiplication of integers only.
Distributive property
According to the distributive property of integers, if a, b and c are integers, then:
a x (b + c) = a x b + a x c
Example: Prove that: 3 x (5 + 1) = 3 x 5 + 3 x 1
LHS = 3 x (5 + 1) = 3 x 6 = 18
RHS = 3 x 5 + 3 x 1 = 15 + 3 = 18
Since, LHS = RHS
Additive Inverse Property
If a is an integer, then as per the additive inverse property of integers,
a + (-a) = 0
Hence, -a is the additive inverse of integer a.
Multiplicative inverse Property
If a is an integer, then as per the multiplicative inverse property of integers,
a x (1/a) = 1
Hence, 1/a is the multiplicative inverse of integer a.
Identity Property of Integers
The identity elements of integers are:
- a+0 = a
- a x 1 = a
Example: -100,-12,-1, 0, 2, 1000, 989 etc…
As a set, it can be represented as follows:
Z= {……-8,-7,-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8,……}
Applications of Integers
Integers are not just numbers on paper; they have many real-life applications. The effect of positive and negative numbers in the real world is different. They are mainly used to symbolize two contradicting situations.
For example, when the temperature is above zero, positive numbers are used to denote temperature, whereas negative numbers indicate the temperature below zero. They help one to compare and measure two things like how big or small or more or fewer things are and hence can quantify things.
Some real-life situations where integers come into play are player’s scores in golf, football and hockey tournaments, the rating of movies or songs, in banks credits and debits are represented as positive and negative amounts respectively.
Integers Related Articles
- Properties Of Integers
- Addition and Subtraction of Integers
- Multiplication and Division of Integers
- Consecutive Integers
- Integers As Exponents
- Operations Of Integers
- Word Problems On Integers
Examples on Integers
Example 1:
Plot the following integers on the number line:
-121, -97, -82, -67, -43, -10, 0, 10, 36, 55, 64, 77, 110, 126, 147.
Solution:

In the above number line, each number has been plotted with a red dot.
Example 2:
Solve the following:
- 5 + 3 = ?
- 5 + (-3) = ?
- (-5) + (-3) = ?
- (-5) x (-3) = ?
Solution:
- 5 + 3 = 8
- 5 + (-3) = 5 – 3 = 2
- (-5) + (-3) = -5 – 3 = -8
- (-5) x (-3) = 15
Example 3:
Solve the following product of integers:
- (+5) × (+10)
- (12) × (5)
- (- 5) × (7)
- 5 × (-4)
Solution:
- (+5) × (+10) = +50
- (12) × (5) = 60
- (- 5) × (7) = -35
- 5 × (-4) = -20
Example 4:
Solve the following division of integers:
- (-9) ÷ (-3)
- (-18) ÷ (3)
- (4000) ÷ (- 100)
Solution:
- (-9) ÷ (-3) = 3
- (-18) ÷ (3) = -6
- (4000) ÷ (- 100) = -40
Practice Questions on Integers
1. Sum of two positive integers is a positive integer. True or False?
2. What is the sum of first five positive integers?
3. What is the product of first five positive odd integers?
4. Plot the integers from -10 to +10 on the number line.
To learn about the properties of integers and to solve problems on the topic, download BYJU’S – The Learning App from Google Play Store and watch interactive videos.
Frequently Asked Questions on Integers
What are integers?
What is an integer formula?
What are the examples of integers?
Can integers be negative?
What are the types of integers?
Zero, Positive integers and Negative integers



Class 7 explain all chapters
The set of positive and negative integers together with 0 is called
Please answer.
Please help me byjus.
The set of positive natural numbers and negative numbers together with 0 is called Integers.
It’s very nice I have the app and I understand it very nicely
We can understand all topics easily in byjus 👍👍👍