In Maths, inverse variation is the relationships between variables that are represented in the form of y = k/x, where x and y are two variables and k is the constant value. It states if the value of one quantity increases, then the value of the other quantity decreases.
In our day-to-day life, we observe that the variation in values of some quantity depends upon the variation in values of some other quantity. Inverse variation means that a variable is inversely varying with respect to another variable. It represents the inverse relationship between two quantities. Hence, a variable is inversely proportional to another variable.
There are many real-life examples of inverse variation, that can be seen in our day to day life. For example:
- If the distance travelled by train at constant speed increases then the time taken by it increases too and vice versa
- If the number of people is added to a job, the time taken to accomplish the job decreases
Inverse Variation Definition
Unlike the direct variation, where one quantity varies directly as per changes in another quantity, in the case of inverse variation, the first quantity varies inversely as per another quantity. Hence, the first quantity is inversely proportional to the other.
Let us say, x and y are two variables, then as per inverse variation:
| y = k/x
or xy = k |
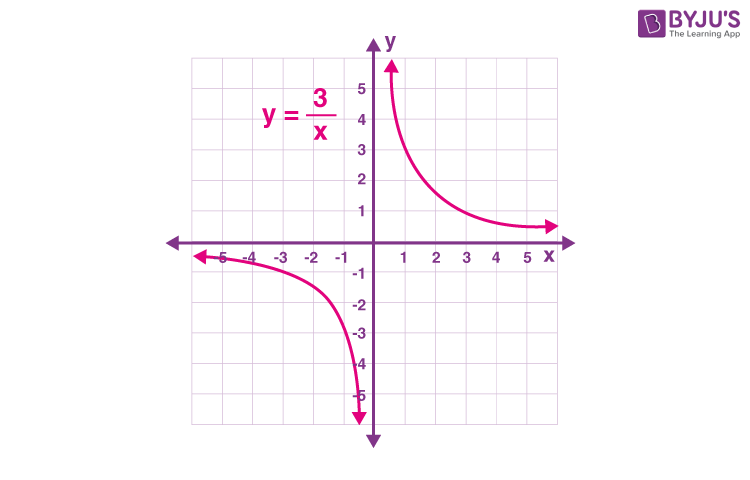
An example of inverse variation, y = 3/x, is represented graphically in the given figure.
Inverse Variation Formula
As per the inverse variation formula, if any variable x is inversely proportional to another variable y, then the variables x and y are represented by the formula:
xy = k or y=k/x
where k is any constant value.
Inverse Variation Equation
Sometimes, we observe that the variation in values of one quantity is just opposite to the variation in the values of another quantity. If the value of one quantity increases, the value of the other quantity decreases in the same proportion and vice versa. This is termed inverse variation and the two quantities are said to be inversely proportional to each other. Two quantities existing in inverse variation can be expressed as,
Where x and y are the value of two quantities and k is a constant known as the constant of proportionality. If x1, y1 are initial values and x2, y2 are final values of quantities existing in inverse variation. They can be expressed as:
\(\begin{array}{l}\frac{x_1}{x_2}~=~\frac{y_2}{y_1}\end{array} \) |
Relation Between Two Quantities in Inverse Variation
In an inverse variation, the relationship between two quantities or variables is defined by inverse proportion. If x and y are two quantities then, the inverse relationship between them is given by:
x ∝ 1/y
or
x = k/y
xy = k
See the examples given below to find the relationship between two quantities in inverse variation.

Inverse Variation Table
The inverse variation table can be written by placing the values of one quantity and finding the other.
For example, y = 10/x
Let us put some values for x and find the value of y.
| x | y = 10/x |
| 1 | 10 |
| 2 | 5 |
| 3 | 3.33 |
| 4 | 2.5 |
| 5 | 2 |
Related Articles
Inverse Variation Solved Examples
Q.1: If x varies inversely with y, and x = 10 and y = 4, then what is the value of constant of variation?
Solution: Given, x varies inversely with y.
Let the constant of variation be k.
x = k/y
or k = xy
But x = 10 and y = 4 (given)
So,
k = 10 x 4 = 40
Hence, the constant of variation is 40.
Q.2: If x and y are in an inverse variation and k/3 = 2, and k/x = 3, then find the value of x when y = 2.
Solution: Given, k/3 = 2
then, k = 3 x 2 = 6
k/x = 3
So, x = k/3 = 6/3 = 2
Hence, if y = 2, then ;
x = k/y = 6/2 = 3
Inverse Variation Word Problems
Example 1: 9 pipes are required to fill a tank in 4 hours. How long will it take if 12 pipes of the same type are used?
Solution: Let, the desired time to fill the tank be
Example 2: If 24 workers can build a house in 40 days, how many workers will be required to build the same house in 20 days?
Solution: Let the number of workers employed to build the wall in 20 days be
Example 3: There are 100 students in a hostel. Food provision for them is for 20 days. After 8 days 20 new students entered the hostel. How long will this provision last now?
Solution: Suppose the provision lasts for x more days after the intrusion of 20 new students which would have lasted for 12 days if the number of students was 100. We know that the time till which food lasts is inversely proportional to the number of students in the hostel. Thus,
Total number of days for which provision lasts =
For a detailed discussion on the concept of inverse variation and Inverse Variation Formula and developing a relationship between two quantities, download BYJU’S – The learning App.


Comments