Basic Proportionality Theorem & Similar Triangles

Basic Proportionality theorem was introduced by a famous Greek Mathematician, Thales, hence it is also called Thales Theorem. According to him, for any two equiangular triangles, the ratio of any two corresponding sides is always the same. Based on this concept, he gave theorem of basic proportionality (BPT). This concept has been introduced in similar triangles.  If two triangles are similar to each other then,

• i) Corresponding angles of both the triangles are equal
• ii) Corresponding sides of both the triangles are in proportion to each other

Learn Basic Mathematics at BYJU’S to clear your concepts and fundamentals.

Thus two triangles ΔABC and ΔPQR are similar if,

• i) ∠A=∠P, ∠B=∠Q and ∠C=∠R
• ii) AB/PQ, BC/QR, AC/PR

Also, read:

Thales Theorem Statement

Let us now state the Basic Proportionality Theorem which is as follows:

If a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio.

Basic  Proportionality Theorem Proof

Let us now try to prove the basic proportionality theorem statement

Consider a triangle ΔABC, as shown in the given figure. In this triangle, we draw a line PQ parallel to the side BC of ΔABC and intersecting the sides AB and AC in P and Q, respectively.

According to the basic proportionality theorem as stated above, we need to prove:

AP/PB = AQ/QC

Construction

Join the vertex B of ΔABC to Q and the vertex C to P to form the lines BQ and CP and then drop a perpendicular QN to the side AB and also draw PM⊥AC as shown in the given figure.

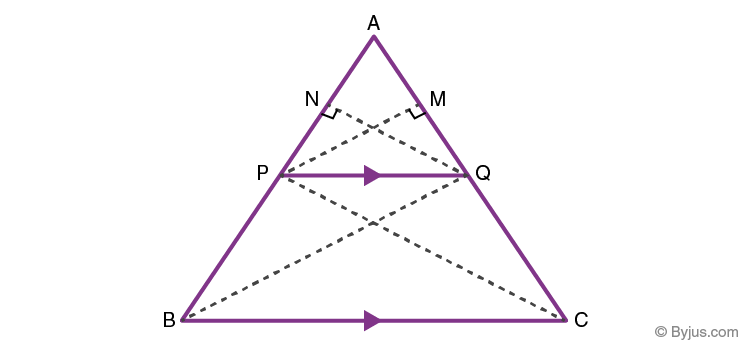
Proof

Now the area of ∆APQ = 1/2 × AP × QN (Since, area of a triangle= 1/2× Base × Height)

Similarly, area of ∆PBQ= 1/2 × PB × QN

area of ∆APQ = 1/2 × AQ × PM

Also,area of ∆QCP = 1/2 × QC × PM ………… (1)

Now, if we find the ratio of the area of triangles ∆APQand ∆PBQ, we have

Similarly,

According to the property of triangles, the triangles drawn between the same parallel lines and on the same base have equal areas.

Therefore, we can say that ∆PBQ and QCP have the same area.

area of ∆PBQ = area of ∆QCP …………..(3)

Therefore, from the equations (1), (2) and (3) we can say that,

AP/PB = AQ/QC

Also, ∆ABC and ∆APQ fulfil the conditions for similar triangles, as stated above. Thus, we can say that ∆ABC ~∆APQ.

The MidPoint theorem is a special case of the basic proportionality theorem.

According to mid-point theorem, a line drawn joining the midpoints of the two sides of a triangle is parallel to the third side.

Consider an ∆ABC.

Conclusion

We arrive at the following conclusions from the above theorem:

If P and Q are the mid-points of AB and AC, then PQ || BC. We can state this mathematically as follows:

If P and Q are points on AB and AC such that AP = PB = 1/2 (AB) and AQ = QC = 1/2 (AC), then PQ || BC.

Also, the converse of mid-point theorem is also true which states that the line drawn through the mid-point of a side of a triangle which is parallel to another side, bisects the third side of the triangle.

Hence, the basic proportionality theorem is proved.

Converse of Basic Proportionality Theorem

According to this theorem, if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

Proof

Suppose a line DE, intersects the two sides of a triangle AB and AC at D and E, such that;

AD/DB = AE/EC ……(1)

Assume DE is not parallel to BC. Now, draw a line DE’ parallel to BC.

Hence, by similar triangles,

AD/DB = AE’/E’C ……(2)

From eq. 1 and 2, we get;

AE/EC = AE’/E’C

Adding 1 on both the sides;

AE/EC + 1 = AE’/E’C +1

(AE +EC)/EC = (AE’+E’C)/E’C

AC/EC = AC/E’C

So, EC = E’C

This is possible only when E and E’ coincide.

But, DE’ || BC

Therefore, DE ||BC.

Hence, proved.

Solved Examples

1. In a ∆ABC, sides AB and AC  are intersected by a line at D and E respectively, which is parallel to side BC. Then prove that AD/AB = AE/AC.

Solution: Given,

DE || BC

So, AD/DB = AE/EC

or we can interchange the ratios as;

DB/AD = EC/AE

Now, add 1 on both sides;

(DB/AD)  + 1 = (EC/AE) + 1

(DB + AD)/AD = (EC + AE)/AE

AB/AD = AC/ AE

If we interchange the ratios again, we get;

AD/AB = AE/AC

Hence, proved.

2. Suppose a triangle ABC, where DE is a line drawn from the midpoint of AB and ends midpoint of AC at E. AD/DB = AE/EC and ∠ADE = ∠ACB. Then prove ABC is an isosceles triangle.

Solution: Given, 

AD/DB = AE/EC

By the converse of basic proportionality theorem, we get;

DE || BC

But it is given that,

∠ADE = ∠ACB

Hence,

∠ABC = ∠ACB

The side opposite to equal angles is also equal.

AB = AC

Hence, ABC is an isosceles triangle.

Solve more such questions by visiting us.

Learning is an unending journey. Paint the canvas of your imagination with the colours of knowledge. Join BYJU’S to keep learning more and more. Visit our website BYJU’S or download BYJU’S -The Learning App.