To understand Mean Absolute Deviation, let us split both the words and try to figure out their meaning. ‘Mean’ refers to the average of the observations and deviation implies departure or variation from a preset standard.
When put together, we can define mean deviation as the mean distance of each observation from the mean of the data.
Mean Absolute Deviation Formula
Ratio of sum of all absolute values of deviation from central measure to the total number of observations.
M.A. D = (Σ Absolute Values of Deviation from Central Measure) / (Total Number of Observations)
Calculate Mean Absolute Deviation
Steps to find the mean deviation from mean:
(i)Find the mean of the given observations.
(ii)Calculate the difference between each observation and the calculated mean
(iii)Evaluate the mean of the differences obtained in the second step.
This gives you the mean deviation from mean.
Suppose that the deviation from a central value a is given as (x-a), where x is any observation of the set of data. To find out the mean deviation, we need to find the average of all the deviations from a in the given data set. Since the measure of central tendency lies between the maximum and minimum values of the data set,we can see that some deviations would be positive and rest would be negative.The sum of such deviations would give a zero. Let us see an example to make this point clearer to you.
Consider the following data set
| Name of student | Maximum Marks(in percentage) |
| Anmol | 85 |
| Kushagra | 75 |
| Garima | 80 |
The mean of the given data is given as:
Now, if we calculate the deviation from mean for the given values, we have:
| Name of student | Maximum Marks(in percentage) | Deviation |
| Anmol | 85 | 85 – 80 = 5 |
| Kushagra | 75 | 75 – 80 = -5 |
| Garima | 80 | 80 – 80 = 0 |
From the definition , we have
This does not give us any idea about measure of variability of the data which is the actual purpose of finding the mean deviation. So, we find the absolute value of deviation from the mean.
In the above example the mean absolute deviation can be calculated as:
This gives us an idea about the deviation of the observations from the measure of central tendency.
Thus we can conclude that,
Although to calculate mean absolute deviation, any measure of central tendency can be used but generally mean and median are the most common ones.
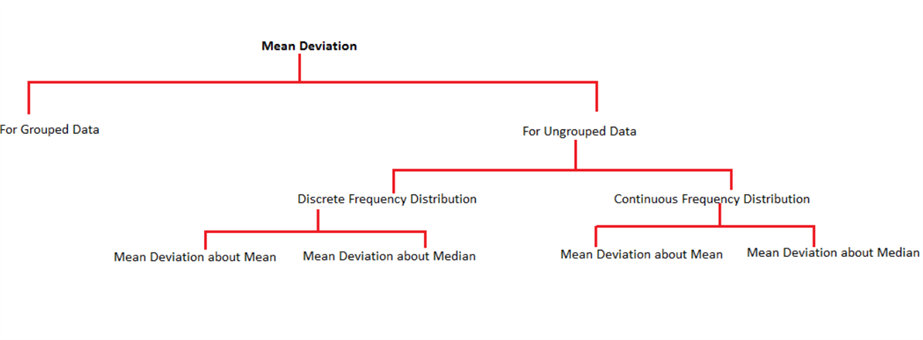
In the upcoming discussions, we will be discussing about calculating deviations for various types of data. The following diagram represents the methods to calculate the mean deviation from mean for two types of data, i.e. grouped and ungrouped data.
Now, you are clear about mean absolute deviation, download Byju’s-the learning app.


Comments