In Maths, the square root of 24 is equal to 2√6 in radical form and 4.898979485 in decimal form. The product of the square root of a number with itself produces the original number. Therefore, the square root is the reverse process of squaring a number. If √24 = x, then x2 = 24. Hence, the square root generates the root value of the original number.
The square root of 24 is denoted by √24, where ‘√’ is the radical symbol and the number under the root is the radicand. Since √2 is an irrational number. Therefore, √24 = 2√6 is also an irrational number.
| Square root of 24 = √24 = ±2√6
Or In decimal form, √24 = 4.898979485 Or In Exponent Form, (24)½ = 4.898979485 |
24 is not a perfect square; it means the square of no natural number generates a value equal to 24. Therefore, the square root of 24 will not be a whole number. Now to find the exact value of √24 we can use the long division method. Although the simplest form of √24 can be evaluated using the prime factorisation method.
| Also check: |
How to Find the Square root of 24?
There are two basic methods, we can use to find the square root of 24:
Prime Factorisation Method
By the prime factorisation method, we can write:
24 = 2 × 2 × 2 × 3
Or we can write the above expression as:
24 = (2 x 2) x 2 x 3
24 = 22 x 2 x 3 [By laws of exponents]
Now, taking square root on both sides, we get;
Taking the square term out of the root, we get;
√24 = 2√6
This is the simplest form of the square root of 24.
We can further put the value of √6 and simplify.
Since, the value of √6 = 2.5 (approx)
Therefore, √24 = 2√6 = 2 x 2.5 ≈ 4.9
Facts:
|
Long Division Method
Long division method is used to find the square root of any number with accuracy. This is also a shortcut method to find the square root of 24. One can easily learn this method and apply it after reading the below-given steps.
- Step 1: Write the number 24 as 24.00 00 00 00
- Step 2: Now, we have to group the digits in a pair of two and place a bar above each pair
- Step 3: Take a number that can be multiplied by itself, such that the resultant is less than or equal to 24. Thus, 4 x 4 = 16
- Step 4: Subtract 16 from 24 to get 8 and add 4 to the previous divisor to get 8. Take down the two zeros and write next to 8 on the dividend side.
- Step 5: Again, take a number and put it at the unit place of the divisor such that when the new divisor is multiplied by that number, it is less than or equal to 800. Thus, 88 x 8 = 704
- Step 6: Repeat the above two steps again and get the quotient up to two places of decimals.
- Therefore, the result is 4.89, as shown in the below diagram
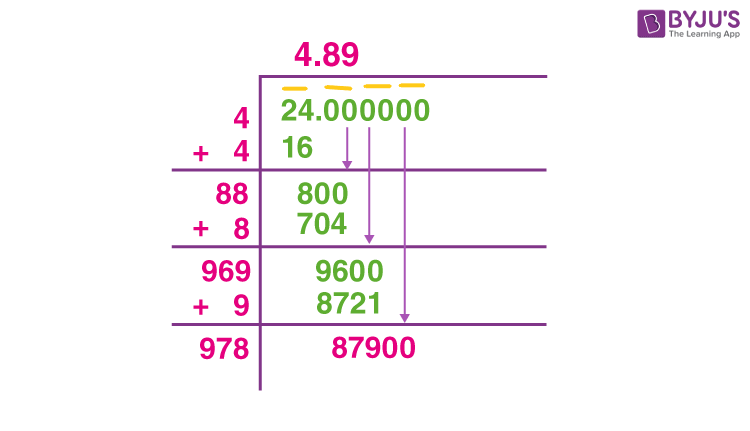
Students can repeat the steps to get the square root value up to four decimal places.
Approximation Method
This method can also be used to find the square root of an imperfect square. It will generate an approximate value which is very close to the actual value of a square root. For one or two-digit numbers, we can use this method to find the square root of them. Since we know the square root of perfect numbers from 1 to 10 as given below:
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
Now, we have to see where the number 24 lies between the squared terms.
Clearly, it lies between 16 and 25, hence between 42 and 52.
Thus, we can conclude that 24 is the square of a number less than 52. Hence, the first digit of √24 is 4.
Now, we have to find the digits after the decimal.
Decimal part = (Actual number- Lower perfect square) /(Higher perfect square-Lower perfect square)
= (24-16)/(25-16)
= 8/9
= 0.88888…
Therefore, the value of √24 = 4.888888…
Or √24 = 4.89
Hence, we have got the correct answer.
Repeated Subtraction Method
Repeated subtraction is also a method of finding the square root. But it is applicable only for perfect squares. Since 24 is a non-perfect square number, therefore we cannot use the method to find its square root.
In repeated subtraction, we subtract consecutive odd numbers starting from the original number till we get a final value equal to zero. The total number of times the subtraction is done will tell us the square root value. If we try this method to find the square root of 24, then;
- 24 – 1 = 23
- 23 – 3 = 20
- 20 – 5 = 15
- 15 – 7 = 8
- 8 – 9 = -1
Since we have got negative integers as a result of subtraction but not zero, therefore we cannot find the square root of 24 here.
Square Roots of Numbers
| √20 | 4.472 |
| √21 | 4.583 |
| √22 | 4.690 |
| √23 | 4.796 |
| √24 | 4.899 |
| √25 | 5.000 |
| √26 | 5.099 |
| √27 | 5.196 |
| √28 | 5.292 |
| √29 | 5.385 |
Video Lessons on Square Roots
Visualising square roots

Finding Square roots

Solved Examples
Q.1: Find the value of 7 multiplied by √24.
Solution: 7 multiplied by √24 is:
7 x √24
Since, the value of √24 = 4.89
Therefore,
7 x √24
= 7 x 4.89
= 34.23
Q.2: Find the length of a chessboard whose area is equal to 24 sq.cm.
Solution: Given, area of chessboard = 24 sq.cm.
Since the chessboard is in square shape. Therefore,
Area of the chessboard = (side)2
Side = (Area)1/2
Side = √24
Side = 2√6 cm.
Hence, the length of the side of the chessboard is 2√6 sq. cm.
Q.3: What is the value of (√24)3?
Solution: The value of (√24)3 is:
(√24)3 = (2√6)3
= 23 x (√6)3
= 8 x 6√6
= 48√6
Q.4: What is five times of the square root of 24?
Solution: Five times of square root of 24 = 5 x √24
⇒ 5 x 4.89
⇒ 24.49
Therefore, five times the square root of 24 is 24.49.
Practice Questions
|
Register with us and download BYJU’S – The Learning App to learn more about squares and square roots with the help of interactive videos.
Frequently Asked Questions on Square root of 24
What is the square root of 24?
The square root of 24 is equal to 2√6 or 4.8989 (up to four places of decimals).
What is the square root of 24 simplified?
Square root of 24 in simplest form is 2√6.
Is 24 a perfect square?
No, 24 is not a perfect square. The square root of 24 is not a natural number.
Is the square root of 24 irrational?
√24 = 4.89897948557, is an irrational number because it is a non-terminating and non-repeating value.
What is the square of 24?
The square of 24 is:
242 = 24 x 24 = 576


Comments