Trigonometry formulas list is provided here based on trigonometry ratios such as sine, cosine, tangent, cotangent, secant and cosecant. These formulas are used to solve various trigonometry problems.
In Mathematics, trigonometry is one of the most important topics to learn. Trigonometry is basically the study of triangles where ‘Trigon’ means triangle and ‘metry’ means measurement.
With reference to a right-angled triangle, the list of trigonometry formulas has been formulated. All the trigonometric formulas are based on identities and ratios. The relationship between angles and length of the sides of the triangle is formulated with the help of trigonometry concepts.
The list of trigonometry based formulas will be helpful for students to solve trigonometric problems easily. Below is the list of formulas based on the right-angled triangle and unit circle, which can be used as a reference to study trigonometry.
List of Important Trigonometry Formulas
First let us learn basic formulas of trigonometry, considering a right-angled triangle, which has an angle θ, a hypotenuse, a side opposite angle to angle θ and a side adjacent to angle θ.

Trigonometric Ratios
So the general trigonometry ratios for a right-angled triangle can be written as;
Trigonometric Ratios for Unit Circle
Similarly, for a unit circle, for which the radius is equal to 1, and θ is the angle. The value of the hypotenuse and adjacent side here is equal to the radius of the unit circle.
Hypotenuse = Adjacent side to θ = 1
Therefore, the ratios of trigonometry are given by:
sin θ = y/1 = y
cos θ = x/1 = x
tan θ = y/x
cot θ = x/y
sec θ = 1/x
cosec θ = 1/y
Trigonometry Identities
Tangent and Cotangent Identities
Reciprocal Identities
sinθ = 1/cosecθ
cosecθ = 1/sinθ
cosθ = 1/secθ
secθ = 1/cosθ
tanθ = 1/cotθ
cotθ = 1/tanθ
Pythagorean Identities
sin2θ + cos2θ = 1
1 + tan2θ = sec2θ
1 + cot2θ = cosec2θ
Even and Odd Angle Formulas
sin(-θ) = -sinθ
cos(-θ) = cosθ
tan(-θ) = -tanθ
cot(-θ) = -cotθ
sec(-θ) = secθ
cosec(-θ) = -cosecθ
Co-function Formulas
sin(900-θ) = cosθ
cos(900-θ) = sinθ
tan(900-θ) = cotθ
cot(900-θ) = tanθ
sec(900-θ) = cosecθ
cosec(900-θ) = secθ
Double Angle Formulas
sin2θ = 2 sinθ cosθ
cos2θ = 1 – 2sin2θ
Half Angle Formulas
Thrice of Angle Formulas
sin3θ = 3sinθ – 4 sin3θ
Cos 3θ = 4cos3θ – 3 cosθ
Sum and Difference Formulas
Sin (A+B) = Sin A Cos B + Cos A Sin B
Sin (A-B) = Sin A Cos B – Cos A Sin B
Cos (A+B) = Cos A Cos B – Sin A Sin B
Cos (A-B) = Cos A Cos B + Sin A Sin B
Product to Sum Formulas
Sin A Sin B = ½ [Cos (A-B) – Cos (A+B)]
Cos A Cos B = ½ [Cos (A-B) + Cos (A+B)]
Sin A Cos B = ½ [Sin (A+B) + Sin (A-B)]
Cos A Sin B = ½ [Sin (A+B) – Sin (A-B)]
Sum to Product Formulas
Inverse Trigonometric Functions
If Sin θ = x, then θ = sin-1 x = arcsin(x)
Similarly,
θ = cos-1x = arccos(x)
θ = tan-1 x = arctan(x)
Also, the inverse properties could be defined as;
sin-1(sin θ) = θ
cos-1(cos θ) = θ
tan-1(tan θ) = θ
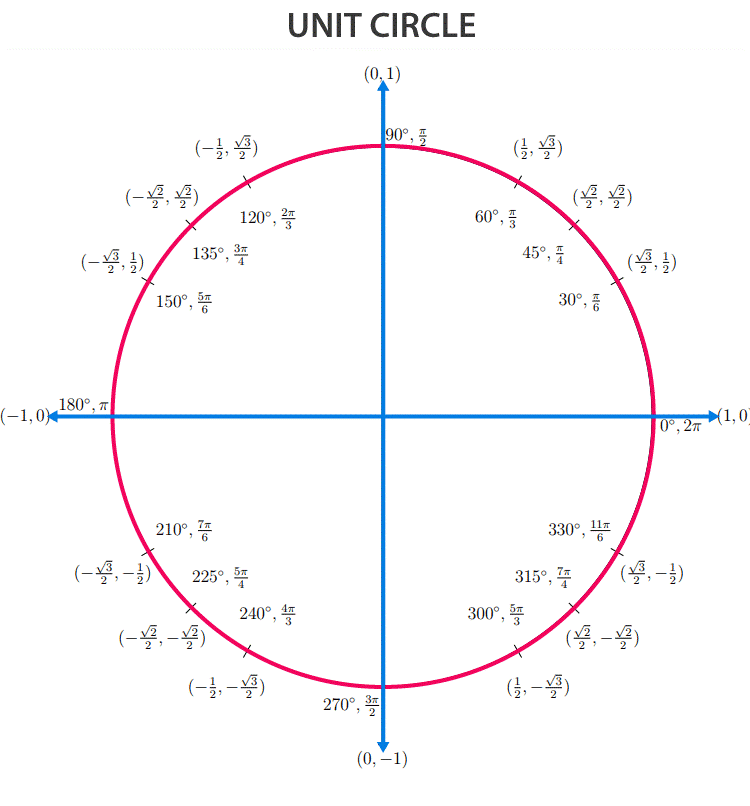
Unit Circle
With the help of unit circle, we can see here the different values of sin and cos ratios for different angles such as 0°, 30°, 45°, 60°, 90°, and so on in all the four quadrants.
Trigonometry Table
| Degrees | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Radians | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| Sin θ | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| Cos θ | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| Tan θ | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| Cot θ | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
| Sec θ | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| Cosec θ | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
Video Lesson on Trigonometry Using Formulas

Learn more Maths formulas with us and Download BYJU’S App for a better learning experience.
| Related Links | |
| Trigonometric Identities | Trigonometric Ratios |
| Trigonometric Equations | Trigonometric Functions |

it’s really helpful recall the formulas and it is easy to teach the formulas. thankyou to byjus
THANK YOU GUYS FOR MAKING TRIGONOMETRY EASY ! ! ! ! ! !
Its very nice
Mathematics all formula PDF send me
Hi,
Please click on Mathematics formulas for Class 10 and get the PDF for all the Maths formulas.