Use of Variables in Common Rules: This part of algebra in Class 6 explained the use of variables in geometry and arithmetic. The rules from both geometry and arithmetic for using variables are provided here with examples.

Check: Variables And Constants In Algebraic Expressions

What are Variables?

In Mathematics, a variable is an alphabetical term that is used to represent an unknown quantity. Variables are an important part of Algebra. Both small letters and capital letters of alphabets can be used to represent the variables.

The most common applications of variables are:

• Algebraic expressions
• Linear Equations
• Geometry

Examples of Variables are:

• 3 + x = 2
• X = 3
• (a+b)² = a² + b² + 2ab

Use of Variables in Geometry

In geometry, we learn about the perimeter of a square and rectangle. Let us use the variables here to represent the perimeters for both the shapes.

Perimeter of Square Rule

Suppose a square that has sides equal to the ‘l’ unit. Here, ‘l’ is a variable.

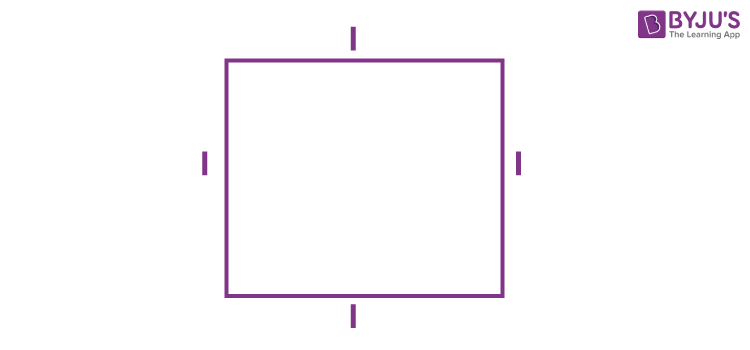
Now by the definition of perimeter, we know that, perimeter of a square is equal to the sum of all the sides. A square has all its four sides equal in length. Therefore,

Perimeter of square = l + l + l + l = 4l

Now, for any value of l, we can find the perimeter of a square. Thus, the use of variable ‘l’, allows use of the perimeter rule in a general way.

For example, the length of the side of a square is 5cm.

Therefore, the perimeter of square = 4l = 4 x 5 = 20 cms

Perimeter of Rectangle Rule

A rectangle is a polygon that has opposite sides equal. Therefore, for the opposite sides we can take the same variable.

Let the length of the opposite sides be a and b, respectively.

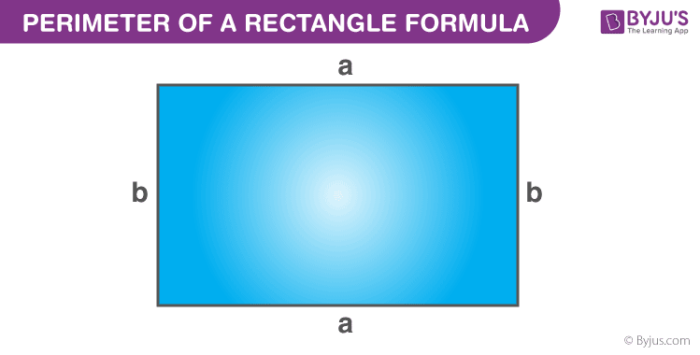
Now, by the definition of perimeter, the formula will be:

Perimeter = Sum of all sides

P = a + b + a + b

P = 2a + 2b

P = 2(a+b)

Here, both a and b are variables. Both the variables are independent of each other. It means the value of a is not dependent on the value of b.

Example: Find the perimeter of a rectangle, with length = 4 cm and width = 3 cm.

Let length of the rectangle, a = 4 cm

width of a rectangle, b = 3cm

Hence,

Perimeter of rectangle = 2 (a + b)

= 2 (4 + 3)

= 2 (7)

= 14 cms

Use of Variables in Arithmetic

Likewise, in arithmetic, the variables have a significant role to represent the unknown values or to describe a property. The three properties explained under use of variables are:

• Commutative property of addition of two numbers
• Commutative property of multiplication of two numbers
• Distributive property

Commutativity of addition of two variables

When we add two numbers together, then the resultant value is equal to the value when the order of the numbers are changed. Commuting means interchanging. Now, if we use the variables for the two numbers as ‘a’ and ‘b’, then it will generalise the property. Hence,

a + b = b + a

Where, a and b are the variables that can take any value.

Example: If a = 10 and b = 2, then,

10 + 2 = 2 + 10 (=12)

Commutativity of multiplication of two variables

When two numbers are multiplied together, then the change of order of numbers, does not change the result of the product. Thus, here also we can generalise the property of commuting numbers in multiplication.

Again using the variables ‘a’ and ‘b’, we can represent the general property of commutativity of multiplication.

a × b = b × a

Where a and b can take any value.

Example: Suppose if a = 4 and b = 8, then;

4 x 8 = 8 x 4 (=32)

Distributivity of numbers

Let us assume that, we have to find the value of 3 x 90. Now, we can write this product form as:

3 x 90 = 3 x (80 + 10) = 3 x 80 + 3 x 10 = 240 + 30 = 270

Also, if we directly multiply 3 by 90, then the value is equal to 270.

Thus, the above rule is applicable to any three numbers.

So, we can generalise the above rule by using three variables say, a, b and c and express it as:

a × (b + c) = a × b + a × c

Where a, b and c can be any three numbers.

Example: If a = 2, b = 5 and c = 10, then;

2 x (5 + 10) = 2 x 5 + 2 x 10 (=30)